Знакочередующиеся числовые ряды. Признак Лейбница.Абсолютная и условная сходимость числового ряда

Ряд называется Знакочередующимся, если он имеет вид: (1)

Теорема (Признак Лейбница):
Если последовательность , n=1,2,.. монотонно убывает, а =0, то ряд (1) сходится.

Замечание.

Ряд (1) , удовлетворяющий условию теоремы Лейбница принято называть Рядом Лейбница.

Ряд Лейбница будет также сходится, если условие монотонности и чередование знака будет выполняться, начиная с n = n0 , но при обязательном условии =0.

Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:

Пусть для знакочередующегося ряда

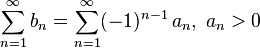
$\sum_{n=1}^\infty b_n = \sum_{n=1}^\infty (-1)^{n-1}\,a_n, \; a_n>0$

выполняются следующие условия:

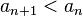$a_{n+1} < a_n$ (монотонное убывание {a_n})
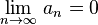$\lim_{n \to \infty} \, a_n = 0$ .

Тогда этот ряд сходится.

Абсолютная и условная сходимость

Ряд 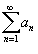 называется абсолютно сходящимся, если ряд  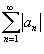также сходится.
Если ряд 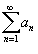 сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.
Ряд 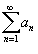 называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.