Рассмотрим функции 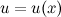 и
и 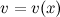 , которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
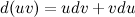
Проинтегрировав левую и правую части последнего равенства, получим:
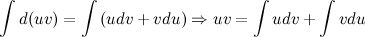
Полученное равенство перепишем в виде:
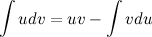
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл 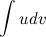 можно свести к нахождению интеграла
можно свести к нахождению интеграла 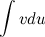 , который может быть более простым.
, который может быть более простым.
Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:
1) 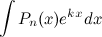 ;
; 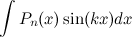 ;
; 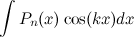
Здесь 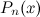 - многочлен степени
- многочлен степени 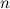 ,
, 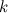 - некоторая константа. В данном случае в качестве функции
- некоторая константа. В данном случае в качестве функции  берется многочлен, а в качестве
берется многочлен, а в качестве 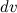 - оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется
- оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется 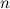 раз.
раз.
2)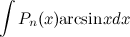 ;
; 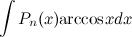 ;
; 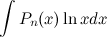
Здесь принимают, что 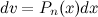 , а в качестве
, а в качестве  оставшиеся сомножители.
оставшиеся сомножители.
3)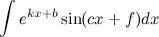 ;
; 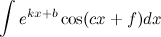
В данном случае в качество  берется либо экспонента, либо тригонометрическая функция. Единственным условием есть то, что при дальнейшем применении формулы интегрирования по частям в качестве функции
берется либо экспонента, либо тригонометрическая функция. Единственным условием есть то, что при дальнейшем применении формулы интегрирования по частям в качестве функции  берется та же функция, то есть либо экспонента, либо тригонометрическая функция соответственно.
берется та же функция, то есть либо экспонента, либо тригонометрическая функция соответственно.
Это способ вычисления неопределенного интеграла, основанный на соотношении (*)
(*)
где u(x) и v(x) – непрерывно дифференцируемые функции, d(u(x)) и d(v(x)) – их дифференциалы.

