Уравнение Пуассона

Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое описывает

электростатическое поле,
стационарное поле температуры,
поле давления,
поле потенциала скорости в гидродинамике.

Проблема расчета электростатического поля в общем случае не является безнадежной. Действительно, если вспомнить выражение векторного поля

через потенциал электростатического поля

(1.65)

то есть

(1.66)

и подставить выражение (1.65) в формулу (1.60), то получим уравнение

(1.67)

Уравнение (1.67) называют уравнением Пуассона, в частном случае

оно превращается в уравнение Лапласа. В операторной форме уравнение Пуассона имеет вид:

(1.68)

где

- оператор Лапласа (лапласиан)

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид: $Delta varphi = f,$

где $Delta$ — оператор Лапласа или лапласиан, а $f$ — вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

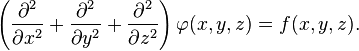
$left( frac{partial^2}{partial x^2} + frac{partial^2}{partial y^2} + frac{partial^2}{partial z^2} right)varphi(x,y,z) = f(x,y,z).$

В декартовой системе координат оператор Лапласа записывается в форме 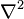$nabla^2$ и уравнение Пуассона принимает вид:

${nabla}^2 varphi = f.$

Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):

$Delta varphi = 0.$

Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».

Уравнение Пуассона является одним из важнейших уравнений электростатики. Нахождение φ для данного f — важная практическая задача, поскольку это обычный путь для нахождения электростатического потенциала для данного распределения заряда. В единицах системы СИ:

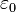${nabla}^2 Phi = - {rho over varepsilon_0},$

где $Phi !$ — электростатический потенциал (в вольтах), $rho !$ — объёмная плотность заряда (в кулонах на кубический метр), а $varepsilon_0 !$ — диэлектрическая проницаемость вакуума (вфарадах на метр).

В единицах системы СГС:

${nabla}^2 Phi = - {4 pi rho}$

В области пространства, где нет непарной плотности заряда, имеем:

$rho = 0, ,$

и уравнение для потенциала превращается в уравнение Лапласа:

${nabla}^2 Phi = 0.$

Потенциал точечного заряда

Потенциал, источником которого служит точечный заряд,

$Phi_q = { 1 over 4 pi varepsilon_0 }{ q over r }$

- то есть кулоновский потенциал - есть по сути (а строго говоря при q = 1) функция Грина

$Phi_1 (x,y,z) = { 1 over 4 pi varepsilon_0 }{ 1 over r }$

для уравнения Пуассона,

то есть решение уравнения

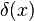$Delta Phi = - { 1 over varepsilon_0 }delta(x)delta(y)delta(z)$

где $delta(x)$ - обозначение дельта-функции Дирака, а произведение трех дельта-функций есть трехмерная дельта-функция, а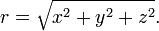 $r = sqrt{x^2+y^2+z^2}.$

В связи с этим ясно, что решение уравнения Пуассона с произвольной правой частью может быть записано как

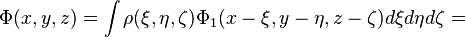
$Phi (x,y,z) = int rho(xi,eta,zeta) Phi_1(x-xi,y-eta,z-zeta) dxi deta dzeta =$

$= int { 1 over 4 pi varepsilon_0 } { rho(xi,eta,zeta) over sqrt{(x-xi)^2+(y-eta)^2+(z-zeta)^2}} dxi deta dzeta.$

Здесь мы имеем в виду наиболее простой случай «без граничных условий», когда принимается, что на бесконечности решение должно стремиться к нулю. Рассмотрение более общего случая произвольных граничных условий и вообще более подробное изложение - см. в статье Функция Грина.
Физический смысл последней формулы - применение принципа суперпозиции (что возможно, поскольку уравнение Пуассона линейно) и нахождение потенциала как суммы потенциалов точечных зарядов $rho dV$ .