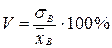Ряды, построенные по количественному признаку, называются вариационным.
Ряды распределений состоят из вариантов (значений признака) и частот (численности групп). Частоты, выраженные в виде относительных величин (долей, процентов) называются частостями. Сумма всех частот называется объёмом ряда распределения.
По виду ряды распределения делятся на дискретные (построены по прерывным значениям признака) и интервальные (построены на непрерывных значениях признака).
Вариационный ряд представляет собой две колонки (или строки); в одной из которых приводятся отдельные значения варьирующего признака, именуемые вариантами и обозначаемые Х; а в другой – абсолютные числа, показывающие сколько раз (как часто) встречается каждый вариант. Показатели второй колонки называются частотами и условно обозначают через f. Еще раз заметим, что во второй колонке могут использоваться и относительные показатели, характеризующие долю частоты отдельных вариантов в общей сумме частот. Эти относительные показатели именуются частостями и условно обозначают через ω Сумма всех частостей в этом случае равна единице. Однако частоты можно выражать и в процентах, и тогда сумма всех частостей дает 100%.
Если варианты вариационного ряда выражены в виде дискретных величин, то такой вариационный ряд именуют дискретным.
Для непрерывных признаков вариационные ряды строятся как интервальные, то есть значения признака в них выражаются «от… до …». При этом минимальны значения признака в таком интервале именуют нижней границей интервала, а максимальное – верхней границей.
Интервальные вариационные ряды строят и для дискретных признаков, варьирующих в большом диапазоне. Интервальные ряды могут быть с равными и неравными интервалами.
Рассмотрим как определяется величина равных интервалов. Введем следующие обозначения:
i – величина интервала;
- максимальное значение признака у единиц совокупности;
– минимальное значение признака у единиц совокупности;
n – число выделяемых групп.
, если n известно.
Если число выделяемых групп трудно заранее определить, то для расчета оптимальной величины интервала при достаточном объеме совокупности может быть рекомендована формула, предложенная Стерджессом в 1926 году:
n = 1+ 3.322 lg N, где N – число единиц в совокупности.
Величина неравных интервалов определяется в каждом отдельном случае с учетом особенностей объекта изучения.
Статистическим распределением выборки называют перечень вариант и соответствующих им частот (или относительных частот).
Статистическое распределение выборки можно задать в виде таблицы, в первой графе которой располагаются варианты , а во второй - соответствующие этим вариантам частоты ni, или относительные частоты Pi .
Статистическое распределение выборки
| Варианты хi | x1 | x2 | x3 | … | xi | … | xk |
| Число наблюдений (частота) ni | n1 | n2 | n3 | … | ni | … | nk |
| Относительная частота Pi | P1 | P2 | P3 | … | Pi | … | Pk |
Интервальными называются вариационные ряды, в которых значения признаков, положенных в основу их образования, выражены в определенных пределах (интервалах). Частоты в этом случае относятся, не к отдельным значениям признака, а ко всему интервалу.
Интервальные ряды распределения строятся по непрерывным количественным признакам, а также по дискретным признакам, варьирующим в значительных пределах.
Интервальный ряд можно представить статистическим распределением выборки с указанием интервалов и соответствующих им частот. При этом в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал.
При группировке по количественным непрерывным признакам важное значение имеет определение размера интервала.
Кроме выборочной средней и выборочной дисперсии применяются и другие характеристики вариационного ряда.
Модой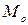 
называют варианту, которая имеет наибольшую частоту.
Например, для ряда
Медианой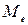 
называют варианту, которая делит вариационный ряд на две части, равные по числу вариант.
Размахом варьирования R называют разность между наибольшей и наименьшей вариантами: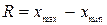 
.
Средним абсолютным отклонением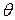 
называют среднее арифметическое абсолютных отклонений: 
.
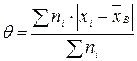Среднее абсолютное отклонение служит для характеристики рассеяния вариационного ряда.
Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней: 
