Неравенство Маркова. Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа А верно неравенство 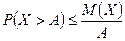 .
.
Доказательство. Расположим значения случайной величины Х в порядке возрастания так, что: 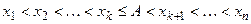 . Математическое ожидание случайной величины примет вид:
. Математическое ожидание случайной величины примет вид: 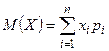 . Отбрасывая первые
. Отбрасывая первые 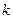 неотрицательных слагаемых и заменяя остальные меньшей величиной А, получим:
неотрицательных слагаемых и заменяя остальные меньшей величиной А, получим: 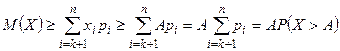 или
или 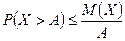 .
.
Пусть ставится задача: оценить вероятность того, что отклонение случайной величины от её математического ожидания не превышает по абсолютной величине положительного числа 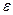 . Если
. Если 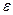 достаточно мало, то можно оценить вероятность того, что Х примет значения достаточно близкие к своему математическому ожиданию. Такая оценка была получена Чебышевым.
достаточно мало, то можно оценить вероятность того, что Х примет значения достаточно близкие к своему математическому ожиданию. Такая оценка была получена Чебышевым.
Неравенство Чебышева. Вероятность того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине меньше положительного числа 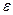 не меньше, чем
не меньше, чем 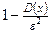 :
: 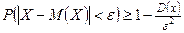 .
.
Доказательство. События 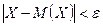 и
и 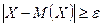 противоположны, тогда
противоположны, тогда 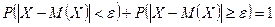 , тогда
, тогда 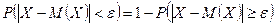 , т.е. надо оценить вероятность
, т.е. надо оценить вероятность 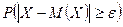 . Для дисперсии случайной величины Х имеем право записать:
. Для дисперсии случайной величины Х имеем право записать:
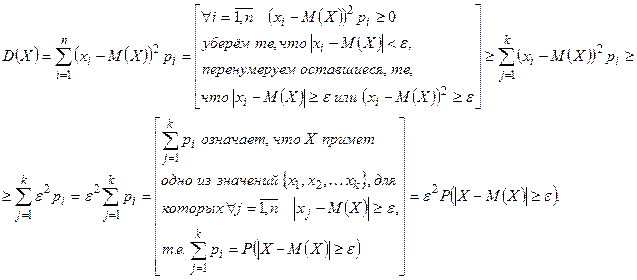
Или 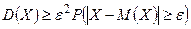 . Тогда
. Тогда 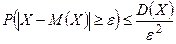 или
или
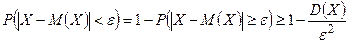 .
.
Замечание 1. Неравенство Чебышева применяется для теоретических исследований.
Замечание 2. Для случайной величины 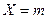 , имеющей биномиальный закон распределения с математическим ожиданием
, имеющей биномиальный закон распределения с математическим ожиданием 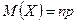 и дисперсией
и дисперсией 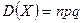
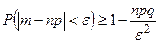 .
.
Замечание 3. Для частоты 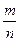 наступления события в
наступления события в 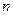 независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью
независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью 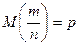 , и имеющей дисперсию
, и имеющей дисперсию 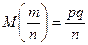
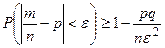 .
.

