Моментом імпульсу матеріальної точки відносно нерухомої точки О називається фізична величина, яка визначається векторним добутком:
Моментом імпульсу відносно нерухомої осі z називається скалярна величина, яка дорівнює проекції на цю вісь вектора моменту імпульсу, визначеного відносно довільної точки О даної осі.
Момент імпульсу твердого тіла відносно осі дорівнює сумі моментів імпульсів окремих частинок:
Продиференціювавши за часом, отримаємо:
Ще одна форма рівняння динаміки обертального руху твердого тіла у векторній формі:
Закон збереження моменту імпульсу: момент імпульсу замкненої системи зберігається:
При рівномірному обертанні твердого тіла відносно деякої осі z закон збереження моменту імпульсу рівносильний:
Моме́нтом і́мпульсу називається векторна величина, яка характеризує інерційні властивості тіла, що здійснює обертальний рух відносно певної точки (початку координат).
Зміст
[сховати]
Момент імпульсу в класичній механіці[ред. • ред. код]
Визначення[ред. • ред. код]
Моментом імпульсу матеріальної точки відносно початку координат в класичній механіці є величина, яка дорівнює векторному добутку радіус-векторацієї частинки на її імпульс.

Відповідно,
- L -- кутовий момент
- r -- радіус-вектор частинки
- p -- імпульс частинки
Якщо фізична система складається з багатьох матеріальних точок, то результуючий момент імпульсу відносно початку координат є сумою (інтегралом) усіх моментів імпульсу складових системи.
Для багатьох практичних задач, які вивчають властивості об'єкта, що обертається навколо певної осі, достатньо проаналізувати скалярне значення момента імпульсу, який є додатним, якщо обертання відбувається проти годинникової стрілки та від'ємним, якщо навпаки.
Відповідно до визначення векторного добутку векторів, скаляр момента імпульсу визначається як:

де θr,p -- кут між r та p, який вимірюється від r до p; такий порядок обходу векторів при визначенні кута є принциповим. Якщо порядок змінити на зворотний, зміниться й знак.
Для тіла сталої маси, яке обертається навколо фіксованої осі, момент імпульсу можна визначити як добуток момента інерції тіла відносно цієї осі на його кутову швидкість:

де I -- момент інерції частинки, ω -- вектор кутової швидкості.
Момент імпульсу у Спеціальній теорії відносності та класичній теорії поля[ред. • ред. код]
У Спеціальній теорії відносності вектор моменту імпульсу дає компоненти антисиметричного тензора другого рангу - тензора моменту імпульсу та спіну:
 ,
,
або, у явному вигляді,
 ,
,
де ![\ \mathbf L = [\mathbf r \times \mathbf p], \quad \mathbf G = \frac{E}{c}\mathbf r - ct \mathbf p](http://upload.wikimedia.org/math/d/e/8/de8b3e6da4ad15b986397605f20bdb65.png) - вектори моменту імпульсу та спіну.
- вектори моменту імпульсу та спіну.
Тензорне представлення вектора моменту імпульсу слідує з того, що перетворення Лоренца даного вектора співпадає з перетворенням Лоренца компонент антисиметричного тензора.
У рамках класичної теорії поля тензором моменту імпульсу та спіну називають струм, який відповідає інваріантності лагранжіану поля по відношенню до перетворень Лоренца, які можна інтерпретувати як повороти у 4-просторі-часі:
 ,
,
де 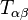 - тензор енергії-імпульсу,
- тензор енергії-імпульсу,  - поле,
- поле,  - величина-похідна, що визначає трансформаційні властивості поля по відношенню до перетворення Лоренца.
- величина-похідна, що визначає трансформаційні властивості поля по відношенню до перетворення Лоренца.
Наявність спінової частини у тензорі моменту імпульсу та спіну тісно пов'язано із симетрією тензора енергії-імпульсу відносно перестановки індексів. Якщо тензор енергії-імпульсу симетричний, то кутова та спінова частини тензору моменту імпульсу та спіну зберігаються (у термінах теорії поля) окремо. Якщо ж провести процедуру "занесення" спінової частини до кутової тензору моменту імпульсу та спіну, то одночасно із цим можна симетризувати тензор енергії-імпульсу. Така процедура називається процедурою Беліфанте. 














Закон збереження момента імпульсу[ред. • ред. код]
Момент імпульсу -- одна з фізичних величин, для якої діє фундаментальний закон збереження.
Назвемо замкненою (в сенсі обертання) таку систему, для якої сума моментів зовнішніх сил M дорівнює нулю. Для такої системи

та
 .
.
Тобто, в замкненій системі момент імпульсу зберігається незмінним. Як випливає з теореми Нетер, таке твердження є наслідком ізотропності (тобто рівноцінності всіх напрямів) простору.
Момент імпульсу в квантовій фізиці[ред. • ред. код]
Докладніше у статті Оператор кутового моменту
В квантовій механіці момент імпульсу визначається не як фізична величина, а як оператор над вектором стану.
Оператор момента імпульсу має вигляд:

де r та p -- оператори радіус-вектора та імпульсу системи. Для вільної частинки без спіну та електричного заряду, оператор момента імпульсу може бути наведений в такій формі:
 , де
, де  -- оператор Гамільтона.
-- оператор Гамільтона.
Окремі компоненти оператора момента імпульсу не комутують між собою. Внаслідок цього їх неможливо визначити одночасно. Детальніше дивись в статті оператор кутового моменту.



 і моментом
і моментом 