.-зав-ть перемещ.токи от вр.наз-ся зак.движ-ия. Для кол-ия з-н движ-ия имеет гармон.хар-р. х=Аcos(ώt+ϕ). В кач-ве осн.для выв-да ур-ия движ-ия исп-ем 2-ой з-н Ньют. F=ma 27.
Колебанияминазывают движения или изменения состояния, повторяющиеся через определенные промежутки времени.
Простейшим видом колебательного движения являются гармонические колебания, когда колеблющаяся величина изменяется со временем по закону синуса или косинуса.
Покажем, что гармоническое колебание возникает под действием упругой силы. Представим материальную точку массой m, закрепленную на пружине жесткости ки расположенную на абсолютно гладкой горизонтальной поверхности (см. рис. 1). Если растянуть пружину на расстояние х, то со стороны пружины на эту точку действует упругая сила Fy , пропорциональная смещению х по закону Гука:
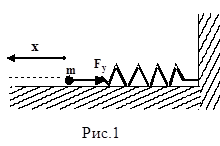 |
Fy = - кх.
Знак “минус” указывает на противоположность направлений смещения и действия силы упругости.
Чтобы установить характер движения, т.е. зависимость х = f(t), запишем для этого случая дифференциальное уравнение, считая что в рассматриваемой системе движение определяется только наличием силы упругости:

