42. Гармонические колебания в колебательном контуре

. d^2q/(dt^2)+1q/LC=0. ώ=sqrt(1/LC) В колеб.кон-ре пр-ит гармон.кол-ия зар-ов,харак-ая част.опр-ся пар-ми контура LCсоот-но энерг.заряж.кон-ра Ec=CU^2/2        

Среди исследований различных электрических явлений особое место занимают исследования электромагнитных колебаний. При колебательном процессе электрические физические величины (заряды, токи) периодически изменяются и процесс сопровождается взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний применяется колебательный контур — цепь, которая состоит из последовательно включенных резистора сопротивлением R, катушки индуктивностью L, и конденсатора емкостью С. 

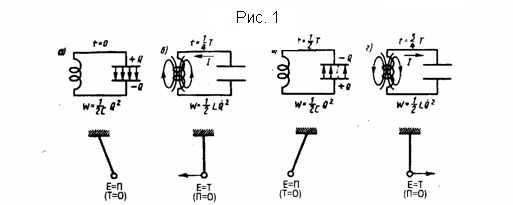
Исследуем последовательные стадии колебательного процесса в идеализированном контуре, у которого сопротивление пренебрежимо мало (R≈0). Для возбуждения колебаний в контуре конденсатор предварительно заряжают, сообщая его обкладкам заряды ±Q. Следовательно, в начальный момент времени t=0 (рис. 1а) между обкладками конденсатора появится электрическое поле, энергия которого равна Q²/(2C) . Если конденсатор замкнуть на катушку индуктивности, то он начнет разряжаться, и в контуре начнет течь возрастающий со временем ток I. В результате энергия электрического поля будет падать, а энергия магнитного поля катушки (она равна (1/2)LI² ) - увеличиваться. 
 

Так как R≈0, то, используя закон сохранения энергии, полная энергия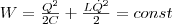 

 

поскольку полная энергия на нагревание не тратится. Поэтому в момент t=(1/4)T, когда конденсатор полностью разрядится, энергия электрического поля станет равной нулю, а энергия магнитного поля (а следовательно, и ток) достигает максимального значения (рис. 1б). Далее, начиная с этого момента ток в контуре будет уменьшаться; значит, начнет уменьшаться магнитное поле катушки, и в ней индуцируется ток, который течет (по правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Далее, начнет перезаряжаться конденсатор, появится электрическое поле, которое будет стремиться ослабить ток, который в конце концов станет равным нулю, а заряд на обкладках конденсатора станет максимальным (рис. 1в). Далее те же процессы будут протекать в обратном направлении (рис. 1г) и к моменту времени t=Т система придет в первоначальное состояние (рис. 1а). После этого рассмотренный цикл разрядки и зарядки конденсатора будет повторяться. Если бы в контуре потерь энергии не было, то совершались бы периодические незатухающие колебания, т.е. периодически изменялись (колебались) бы заряд Q на обкладках конденсатора, сила тока I, текущего через катушку индуктивности и напряжение U на конденсаторе . Значит, в контуре появляются электрические колебания, причем колебания сопровождаются превращениями энергий электрического и магнитного полей. 

С электрическими колебаниями в колебательном контуре можно провести аналогию с механическими колебаниями маятника (рис. 1 внизу), которые сопровождаются взаимными превращениями кинетической и потенциальной энергий маятника (на рисунке Е - кинетическая энергия, П - потенцияльная). В данном случае энергия электрического поля конденсатора Q²/(2C) аналогична потенциальной энергии маятника, энергия магнитного поля катушки (LQ²/2) — кинетической энергии, сила тока в контуре — скорости движения маятника. Индуктивность L аналогична массе m, а сопротивление контура — силе трения, которая действуюет на маятник. 

По закону Ома, для контура, который содержит резистор сопротивлением R, катушку индуктивностью L, и конденсатор емкостью С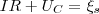 

 

где IR—напряжение на резисторе, U_C = Q/C - напряжение на конденсаторе, ξ_s = -L(dI/dt) – э.д.с. самоиндукции, которая возникает в катушке при протекании в ней переменного тока (ξ_s – единственная э.д.с. в контуре). Значит,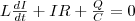 

 (1) 

Разделив формулу (1) на L и подставив 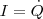 и 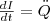 получим дифференциальное уравнение колебаний заряда Q в контуре: 

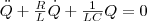 (2) 

В рассматриваемом колебательном контуре внешние э.д.с. отсутствуют, значит колебания в контуре представляют собой свободныеколебания. Если сопротивление R=0, то свободные электромагнитные колебания в контуре будут гармоническими. Тогда из (2) найдем дифференциальное уравнение свободных гармонических колебаний заряда в контуре: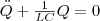 

 

Из формулы (1) следует, что заряд Q гармонически колеблеься по закону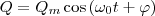 

 (3) 

где Q_m — амплитуда колебаний заряда конденсатора с циклической частотой ω₀, которая называется собственной частотой контура, т. е.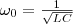 

 (4) 

и периодом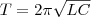 

 (5) 

Выражение (5) впервые было получено У. Томсоном и называется формулой Томсона. Сила тока в колебательном контуре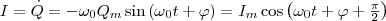 

 (6) 

где I_m = ω₀Q_m — амплитуда силы тока. Напряжение на конденсаторе равно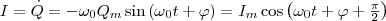 

 (7) 

где U_m=Q_m/C - амплитуда напряжения. 

Из формул (3) и (6) вытекает, что колебания тока I опережают по фазе колеба