Основное ур-е нерелятив.квант.механики:
-∆ψ+Uψ=i ħ, где U=U(x,y,z,t)-потенциальная функция,∆-оператор Лапласа,i-мнимая единица.Искомая волновая ф-я должна обл. след.св-ами:непрерывность,конечность,однозначность.ψ2должна быть интегрируемой.
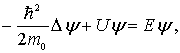 |
(4.5) |
где 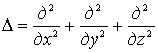 - оператор Лапласа. Уравнение (4.5) называется уравнением Шредингера для стационарных состояний. Его решения - функции
- оператор Лапласа. Уравнение (4.5) называется уравнением Шредингера для стационарных состояний. Его решения - функции 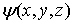 и соответствующие значения энергии
и соответствующие значения энергии 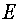 - определяются конкретным видом потенциальной энергии частицы
- определяются конкретным видом потенциальной энергии частицы 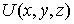 . Часто уравнение Шредингера для стационарных состояний записывают в следующей форме
. Часто уравнение Шредингера для стационарных состояний записывают в следующей форме
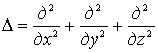 - оператор Лапласа. Уравнение (4.5) называется уравнением Шредингера для стационарных состояний. Его решения - функции
- оператор Лапласа. Уравнение (4.5) называется уравнением Шредингера для стационарных состояний. Его решения - функции 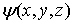 и соответствующие значения энергии
и соответствующие значения энергии 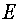 - определяются конкретным видом потенциальной энергии частицы
- определяются конкретным видом потенциальной энергии частицы 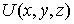 . Часто уравнение Шредингера для стационарных состояний записывают в следующей форме
. Часто уравнение Шредингера для стационарных состояний записывают в следующей форме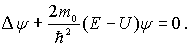 |
(4.6) |
Перейдем теперь к анализу временной функции 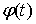 . Решение уравнения (4.4b) имеет вид
. Решение уравнения (4.4b) имеет вид
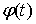 . Решение уравнения (4.4b) имеет вид
. Решение уравнения (4.4b) имеет вид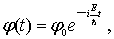 |
(4.7) |
где 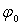 - некоторая константа.
- некоторая константа.
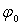 - некоторая константа.
- некоторая константа.
