Гармонические колебания. Период, частота и фаза. Их связь с начальными условиями и параметрами системы. Энергия колебательного движения.

Консервативный гармонический осциллятор

В качестве модели консервативного гармонического осциллятора возьмём груз массы m, закреплённый на пружине жёсткостью k.

Пусть x — смещение груза относительно положения равновесия. Тогда, согласно закону Гука, на него будет действовать возвращающая сила:

$F = -k x. \,$

Используя второй закон Ньютона, запишем

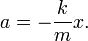
$a = -\frac{k}{m}x. \,$

Обозначая ${\omega_0}^2 = k/m$ и заменяя ускорение a на вторую производную от координаты по времени $\ddot x,$ напишем:

$\ddot x + \omega_0^2 x = 0.$

Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Коэффициент $\omega_0$ называют циклической частотой осциллятора. (Здесь имеется в виду круговая частота, измеряющаяся в радианах в секунду. Чтобы перевести её в частоту, выражающуюся в Герцах, надо разделить круговую частоту на $2 \pi$ )

Будем искать решение этого уравнения в виде:

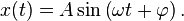
$x(t) = A \sin\left(\omega t + \varphi\right).$

Здесь A — амплитуда, ω — частота колебаний (пока не обязательно равная собственной частоте), φ — начальная фаза.

Ускорение может быть также выражено как функция перемещения:

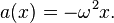
$a(x) = -\omega^2 x.\!$

Поскольку ma = −mω²x = −kx, то

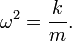
$\omega^2 = \frac{k}{m}.$

Учитывая, что ω = 2πf, получим

$f = \frac{1}{2\pi}\sqrt{\frac{k}{m}},$

и поскольку T = 1/f, где T — период колебаний, то

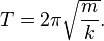
$T = 2\pi\sqrt{\frac{m}{k}}.$

Эти формулы показывают, что период и частота не зависят от амплитуды и начальной фазы движения.

ТУТА НЕ ВСЁ ЕСТЬ