5. необходимое и достаточное условие возрастания и убывания функции на интервале.
http://glaznev.sibcity.ru/1kurs/der/html/lek_d7.htm
Листаем ниже на сайте, что то есть.
6.Необходимое и достаточное и достаточное условие экстремума ф-ции
http://glaznev.sibcity.ru/1kurs/der/html/lek_d7.htm
ниже на сайте
7. Производная произведений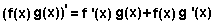 
8.Производная частного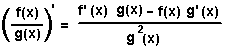 
9.Производная y=Lnx 
10. Производная Sinx
11. Производная cosx
12. Производная arcsinx 
13. Производная arctgx
14. Первый замечательный предел
http://ru.wikipedia.org/wiki/%C7%E0%EC%E5%F7%E0%F2%E5%EB%FC%ED%FB%E5_%EF%F0%E5%E4%E5%EB%FB
15.Второй замечатальный предел
http://ru.wikipedia.org/wiki/%C7%E0%EC%E5%F7%E0%F2%E5%EB%FC%ED%FB%E5_%EF%F0%E5%E4%E5%EB%FB
Часть 2
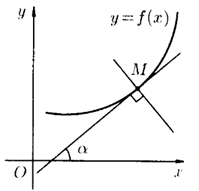
1. Геометрический смысл производной
Производная функции 
, вычисленная при заданном значении 
, равна тангенсу угла, образованного положительным направлением оси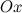 
и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой :
2.Предел функции и его св-ва
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Свойства
http://www.webmath.ru/poleznoe/formules_7_12.php
3.Непрерывность функции
Функция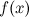 
называется непрерывной в точке 
, если:
- функция 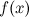определена в точке и ее окрестности;
- существует конечный предел функции 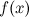в точке ;
- это предел равен значению функции в точке , т.е.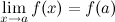
4. дифференциал функции
Дифференциалом функции называется линейная относительно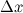 
часть приращения функции. Она обозначается как 
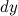или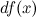 
. Таким образом:
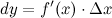
5. бесконечно малые функции и бесконечно малая числовая последовательность
Функция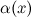 
называется бесконечно малой функцией (б.м.ф.) при 
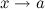(или в точке 
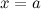), если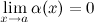
Основные свойства бесконечно малых функций
1° Сумма конечного числа б.м функций является функцией б.м.
2° Произведение б.м функции на ограниченную есть функция б.м.
3° Произведение двух б.м функций есть функция б.м.
4° Произведение б.м функции на константу является б.м функцией.
5° Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.
6° Функция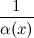 
, обратная к б.м функции 
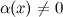, есть функция бесконечно большая. Верно и обратное.
бесконечно малая числовая последовательность
http://glaznev.sibcity.ru/1kurs/lim/htm_lim/lim_lek1.htm
http://www.webmath.ru/poleznoe/formules_7_5.php ????
6.Эквивалентыне фунцкии
Б.м. функци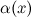и и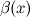 
называются эквивалентными или равносильными б.м. одного порядка при 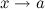, если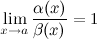 
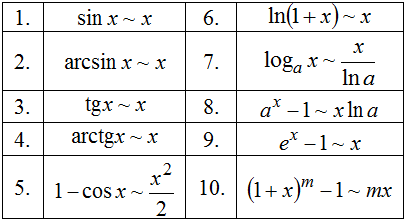
Обозначают: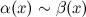 
при .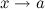
