Теорема: Пусть числовой ряд
|
u1+u2+...+un+... , |
(1) |
сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член un стремится к нулю .
Простейшие свойства сходящихся рядов.
1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.
2. Если ряд 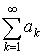 сходится, то
сходится, то 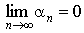 .
.
3. Если ряд 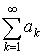 сходится, то сходится ряд
сходится, то сходится ряд 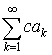 и имеет место равенство
и имеет место равенство
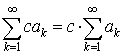 .
.
4. Если ряды 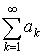 и
и 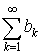 сходятся, то сходится и ряд
сходятся, то сходится и ряд 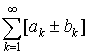 имеет место равенство
имеет место равенство
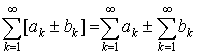 .
.
5. Если ряд 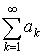 сходится, то
сходится, то 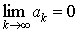 .
.
Отсюда следует
Признак расходимости ряда. Если 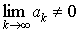 , то ряд
, то ряд 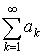 расходится.
расходится.

