Понятие числового ряда и его сходимости. Примеры сходящихся и расходящихся рядов

Определение:

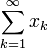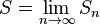Частной суммой числового ряда $\sum_{k=1}^{\infty} x_k$ называется сумма $S_n=\sum_{k=1}^n x_k$ . Числовой ряд называется сходящимся, если существует предел $S = \lim_{n\to\infty} S_n$ , при этом $S$ называется суммой ряда.

Критерий Коши сходимости числового ряда:

Теорема:

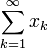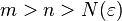
Числовой ряд $\sum_{k=1}^{\infty} x_k$ сходится тогда и только тогда, когда для любого $\varepsilon > 0$ существует такое $N(\varepsilon)$ , что для всех $m > n > N(\varepsilon)$

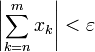
$\left|\sum_{k=n}^m x_k \right| < \varepsilon$

Здесь: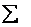
– математический значок суммы;
х_k– общий член ряда (запомните этот простой термин);
k – переменная-«счётчик». Запись 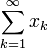$\sum_{k=1}^{\infty} x_k$ обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала у нас 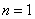, затем 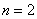, потом 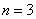, и так далее – до бесконечности.

Доказательство:

Заметим, что 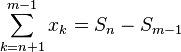$\sum_{k=n+1}^{m-1} x_k = S_n - S_{m-1}$ . После этого утверждение превращается в критерий Коши сходимости последовательности $S_n$ .

Необходимое условие сходимости:

Теорема:

Если ряд 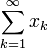$\sum_{k=1}^{\infty} x_k$ сходится, то $\lim_{n\to\infty}x_n = 0$ .

Доказательство:

Из свойств пределов следует, что 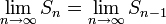$\lim_{n\to\infty} S_n = \lim_{n\to\infty} S_{n-1}$ . Отсюда следует, что $\lim_{n\to\infty} x_n = \lim_{n\to\infty} (S_n - S_{n-1}) = 0$ .