Замена переменной и интегрирование по частям в определенном интеграле

Метод замены переменного в определенном интеграле.

Теорема 5. Пусть функция f(x) непрерывна на интервале (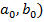, а функция  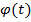имеет непрерывную производную на интервале 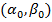, причем  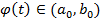при всех .

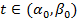Тогда если 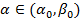, , 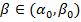, , 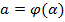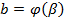т справедлива формула замены переменного в определенном интеграле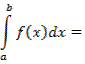

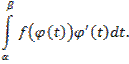
 Так как 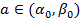, , 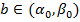а функция f(x) непрерывна на интервале 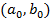, то по формуле Ньютона-Лейбница находим

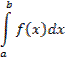=Ф(b)‑Ф(a)

Где 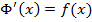 для всех .

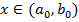            Функция 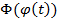 является первообразной для функции, стоящей под знаком интеграла в правой части формулы условия теоремы, так как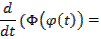

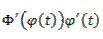
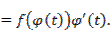
Применяя к функции 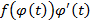 формулу Ньютона-Лейбница и учитывая, что 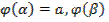=b, получаем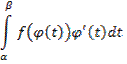
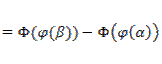=Ф(b)‑Ф(a)

Из последнего и первого равенств доказательства следует формула замены переменного в определенном интеграле.

2)Интегрирование по частям в определенном интеграле.

Терема 6. Если функции u(x) и v(x) имеют на отрезке 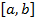 непрерывные производные, то справедлива формула интегрирования по частям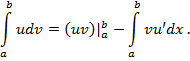

Интегрируя на отрезке 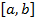 тождество

где 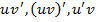  - непрерывные функции, получаем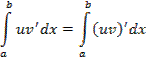

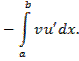
По формуле Ньютона-Лейбница находим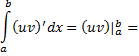

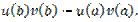
Поэтому предпоследнее равенство можно записать в виде формулы интегрирования по частям.