График функции 
, дифференцируемой на интервале 
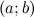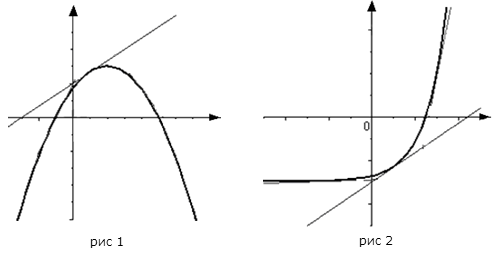
, является на этом интервале выпуклым, если график этой функции в пределах интервала 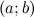лежит не выше любой своей касательной (рис. 1).
Теорема:
(Об условиях выпуклости графика функции)
Пусть функция определена на интервале 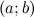и имеет непрерывную, не равную нулю в точке
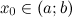вторую производную. Тогда, если 
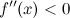, то функция имеет выпуклость.
Определение:
Точкой перегиба графика функции называется точка 
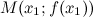, разделяющая промежутки выпуклости и вогнутости.
Теорема:
(О необходимом условии существования точки перегиба)
Если функция имеет перегиб в точке 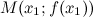, то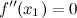 
или не существует.
Теорема:
(О достаточном условии существования точки перегиба)
Если:
- первая производная
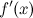непрерывна в окрестности точки 
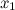; - вторая производная
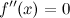или не существует в точке ; 
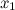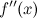при переходе через точку 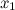меняет свой знак,
тогда в точке 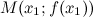функция имеет перегиб.
Схема исследования функции на выпуклость, вогнутость
- Найти вторую производную функции.
- Найти точки, в которых вторая производная равна нулю или не существует.
- Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.
