Определение:
Дифференциалом функции называется линейная относительно 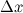 часть приращения функции. Она обозначается как
часть приращения функции. Она обозначается как 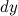 или
или 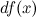 . Таким образом:
. Таким образом:
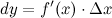
Замечание:
1.Дифференциал функции составляет основную часть ее приращения.
2.Пусть функция  дифференцируема в точке
дифференцируема в точке  , то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно
, то есть приращение этой функции можно представить в виде суммы двух слагаемых: линейного относительно 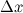 и нелинейного членов:
и нелинейного членов:
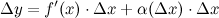
где 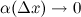 при
при 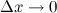 .
.
3.Наряду с понятием дифференциала функции вводится понятие дифференциала аргумента. По определению дифференциал аргумента есть приращение аргумента:
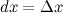
4.Формулу для дифференциала функции можно записать в виде:
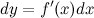
Отсюда получаем, что
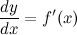
Итак, это означает, что производная может быть представлена как обыкновенная дробь - отношение дифференциалов функции и аргумента.
Геометрический смысл дифференциала
Дифференциал функции в точке 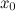 равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента
равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента 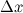 .
.
 На графике функции
На графике функции  возьмем произвольную точку
возьмем произвольную точку  и дадим аргументу
и дадим аргументу  приращение
приращение  . При этом функция получит приращение
. При этом функция получит приращение  (на рисунке отрезок
(на рисунке отрезок  ).
).
Проведем касательную к кривой  в точке
в точке  и обозначим угол ее наклона к оси
и обозначим угол ее наклона к оси  через
через  , тогда
, тогда  . Из треугольника
. Из треугольника  находим
находим 
 , т.е.
, т.е.  .
.
Таким образом, дифференциал функции численно равен приращению ординаты касательной, проведенной к графику функции  в данной точке, когда аргумент
в данной точке, когда аргумент  получает приращение
получает приращение  .
.

