Производная степенной функции
Формула:
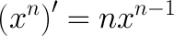
Производная степенной функции равна произведению показателя степени и основания в степени на единицу меньше.
Заметим, что в качестве степени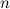 
может быть как натуральное число, то есть 1, 2, 3, ...; так и любое отрицательное число: - 1, - 2 и т.д., а также и любое дробное, например, 2,34; - 4,1 или 
, 
.
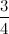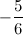Заметим, что если аргумент у степенной функции есть сложная функция (то есть там стоит более сложное выражение, чем просто 
), то производную нужно находить по следующей формуле:
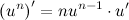
Логарифмическая производная
Логарифмическая производная – производная от натурального логарифма модуля (абсолютной величины) – данной функции: 
Используя формулу производной сложной функции, найдем, что
(*)
Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции.
Пример
Логарифмическая производная функции имеет экономический смысл – отношение скорости изменения величины у (ее производной) к самой этой величине – темп изменения у; если темп положителен – скорость изменения увеличивается, если отрицателен – скорость падает.
