Пусть функции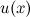 
и 
и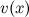меют производные в точке 
. Тогда
1. Константу можно выносить за знак производной.
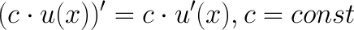
Пример:
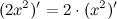
2. Производная суммы/разности.
Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.
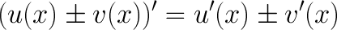
Пример:
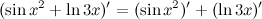
3. Производная произведения.
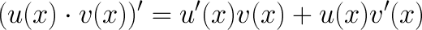
Пример:
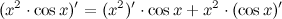
4.Производная частного.
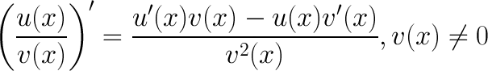
Пример:
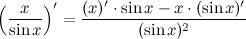
5. Производная сложной функции.
Производная сложной функции равна производной этой функции по промежуточному аргументу 
, умноженной на производную от промежуточного аргумента по основному аргументу .
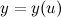и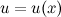 
имеют производные соответственно в точках 
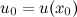и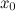 
. Тогда
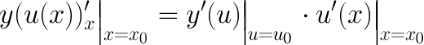
Теорема:
(О производной обратной функции)
Если функция 
непрерывна и строго монотонна в некоторой окрестности точки 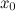и дифференцируема в этой точке, то обратная функция 
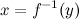имеет производную в точке 
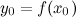, причем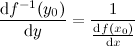 
Вычисление производной функции
Вычисление производной функции у = f(x) производится по следующей схеме:
1) Находим приращение функции на отрезке 
: 
2) Делим приращение функции на приращение аргумента: 
3) Находим предел 
устремляя 
к нулю. Переход к пределу мы будем записывать с помощью знака lim:
