Определение точки разрыва:
Точка 
, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
- функция
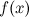определена в точке и ее окрестности; - существует конечный предел функции 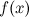в точке ;
- это предел равен значению функции в точке , т.е.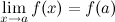
называется точкой разрыва функции.
Пример:
Функция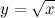 
не определена в точке 
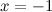, а значит, эта точка является точкой разрыва указанной функции.
Классификация:
1.Точка разрыва первого рода
Определение:
Если в точке существуют конечные пределы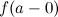 
и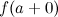 
, такие, что 
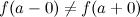, то точка называется точкой разрыва первого рода.
Пример:
Функция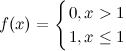 
в точке 
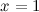имеет разрыв первого рода, так как
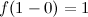, а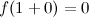 
2.Точка разрыва второго рода
Определение:
Если хотя б один из пределов 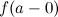или 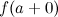не существует или равен бесконечности, то точка называется точкой разрыва второго рода.
Пример:э
Для функции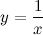 
точка 
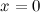- точка разрыва второго рода, так как 
.
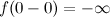3.Точка устранимого разрыва
Определение:
Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции 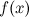в точке : 
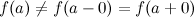или функция 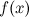не определена в точке , то точка называется точкой устранимого разрыва.
Пример:
Рассмотрим функцию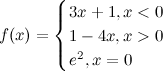 
. Найдем односторонние пределы и значение функции в точке :
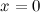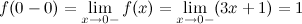
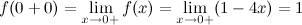
Так как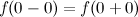 
и не равны значению функции в точке, то точка 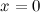- точка устранимого разрыва.
