Терема:
Если функция в точке
имеет предел, то этот предел единственный.
Последовательность точек расширенной числовой прямой 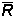 может иметь на этой прямой только один предел.
может иметь на этой прямой только один предел.
Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
 Þ
Þ 
 .
.
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).
 Þ
Þ 
 .
.
Теорема 3. Предел постоянной равен самой постоянной.
 .
.
Доказательство. f(x)=с, докажем, что  .
.
Возьмем произвольное e>0. В качестве d можно взять любое
положительное число. Тогда при 
 .
.
Теорема 4. Функция не может иметь двух различных пределов в
одной точке.
Доказательство. Предположим противное. Пусть
 и
и  .
.
По теореме о связи предела и бесконечно малой функции:
f(x)-A= - б.м. при
- б.м. при  ,
,
f(x)-B= - б.м. при
- б.м. при  .
.
Вычитая эти равенства, получим:
B-A= -
- .
.
Переходя к пределам в обеих частях равенства при  , имеем:
, имеем:
B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.
Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при  , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при  , причем предел алгебраической суммы равен алгебраической сумме пределов.
, причем предел алгебраической суммы равен алгебраической сумме пределов.



 .
.
Доказательство. Пусть  ,
,  ,
,  .
.
Тогда, по теореме о связи предела и б.м. функции:
 где
где  - б.м. при
- б.м. при .
.
Сложим алгебраически эти равенства:
f(x)+g(x)-h(x)-(А+В-С)= ,
,
где  б.м. при
б.м. при  .
.
По теореме о связи предела и б.м. функции:
 А+В-С=
А+В-С=

 .
.
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при  , то и произведение имеет предел при
, то и произведение имеет предел при , причем предел произведения равен произведению пределов.
, причем предел произведения равен произведению пределов.


 .
.
Следствие. Постоянный множитель можно выносить за знак предела.


 .
.
Теорема 7. Если функции f(x) и g(x) имеют предел при  ,
,
причем  , то и их частное имеет предел при
, то и их частное имеет предел при  , причем предел частного равен частному пределов.
, причем предел частного равен частному пределов.
 ,
,  .
.
Предел сложной функции

