Функция  называется бесконечно большой при
называется бесконечно большой при  , если
, если  .
.
Теорема:
Если f(x)®0 при х®а (если х®¥ ) и не обращается в ноль, то
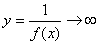
Свойства:
- Сумма бесконечно больших последовательностей одного знака есть бесконечно большая последовательность того же знака.
- Сумма бесконечно большой и ограниченной последовательностей есть бесконечно большая последовательность.
- Произведение бесконечно больших последовательностей есть бесконечно большая последовательность.
- Произведение бесконечно большой последовательности на константу есть бесконечно большая последовательность.
Теорема о связи между бесконечно большой и бесконечно малой функциями:
Если функция 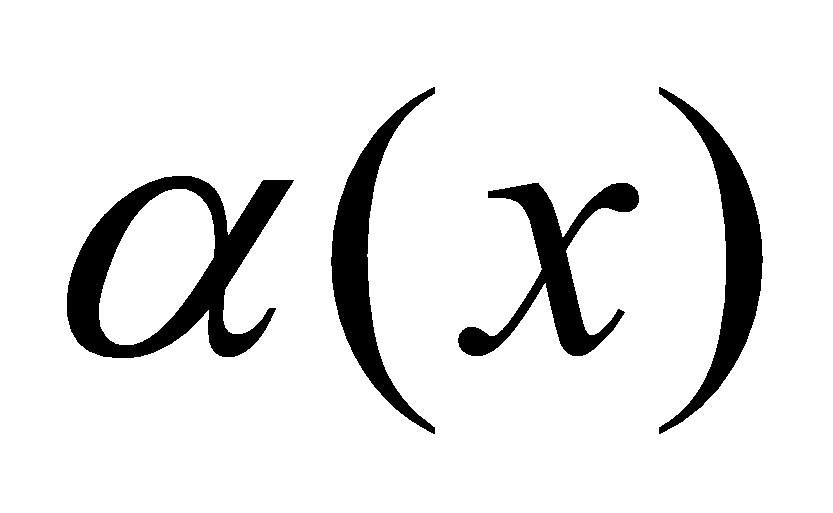 - функция бесконечно малая (
- функция бесконечно малая (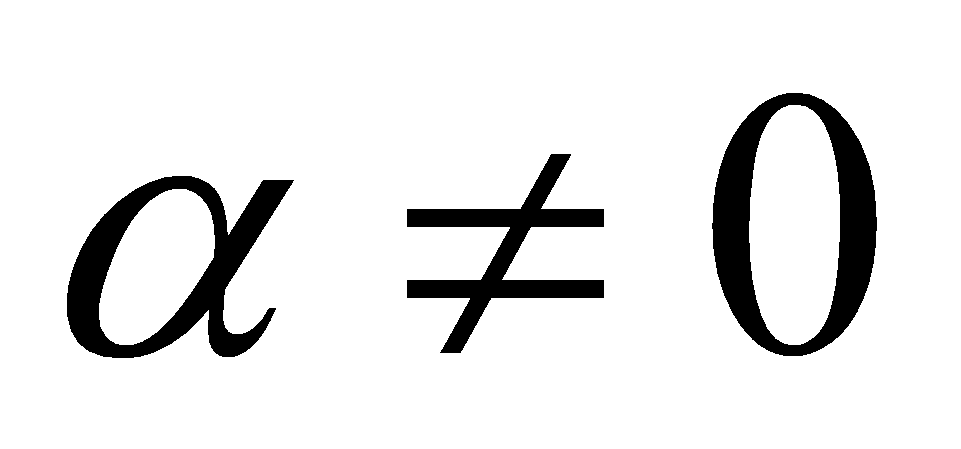 ), то функция
), то функция 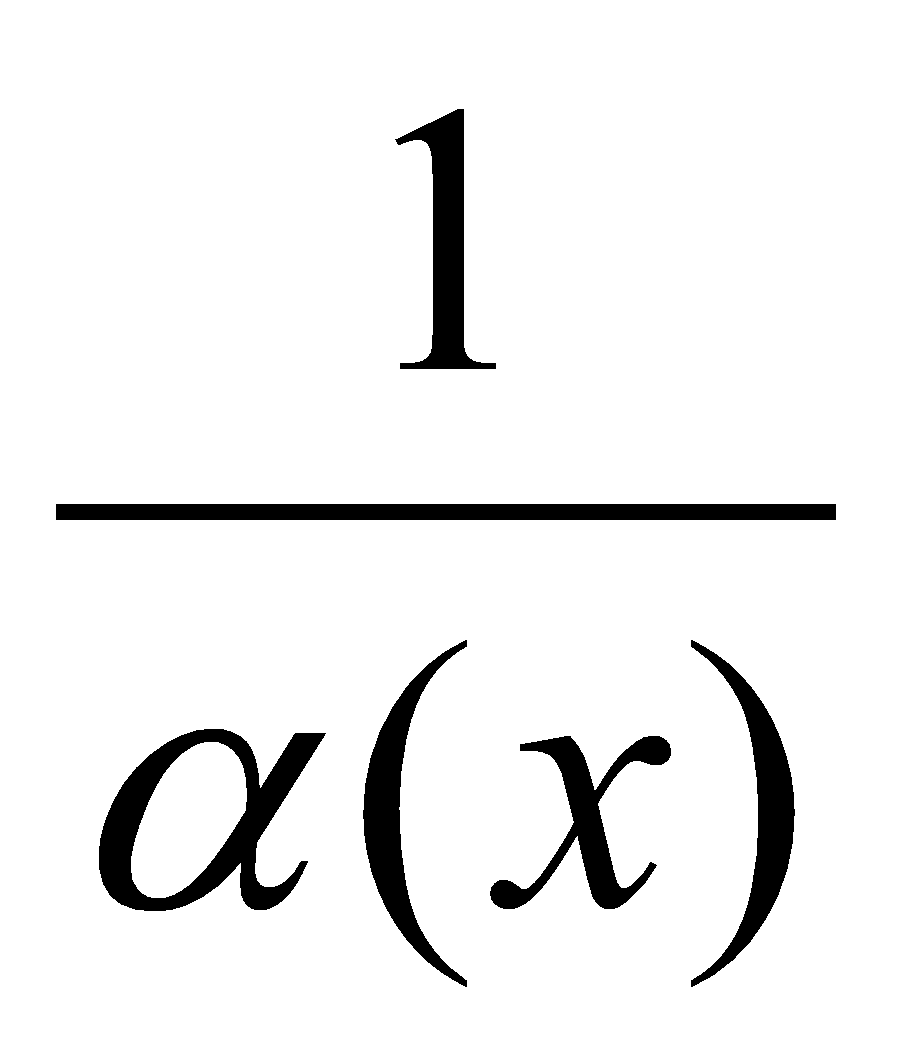 есть бесконечно большая функция и наоборот.
есть бесконечно большая функция и наоборот.

