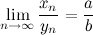Последовательность 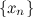 называется сходящейся, если существует такое число
называется сходящейся, если существует такое число 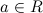 такое, что последовательность
такое, что последовательность 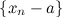 является бесконечно малой последовательностью.
является бесконечно малой последовательностью.
Число  называется пределом последовательности
называется пределом последовательности 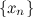 и обозначается
и обозначается 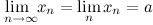 ,
,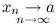
Число  называется пределом последовательности
называется пределом последовательности 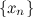 , если для любого
, если для любого 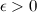 существует номер
существует номер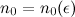 такой, что для любого
такой, что для любого 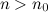 выполняется неравенство
выполняется неравенство 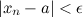 :
:
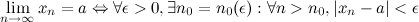
Целой частью 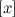 некоторого числа
некоторого числа  называется наибольшее целое число, не превосходящее
называется наибольшее целое число, не превосходящее  .
.
Сходящиеся и расходящиеся последовательности
Последовательность, которая имеет предел, называется сходящейся; иначе - расходящейся.
Теорема:
Сходящаяся последовательность имеет только один предел.
Теорема:
(Необходимый признак сходимости последовательности).
Сходящаяся последовательность ограничена.
Последовательность на бесконечности
Последовательность 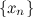 имеет бесконечный предел, если для любого
имеет бесконечный предел, если для любого 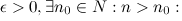
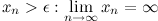
Последовательность 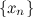 называется бесконечно малой, если
называется бесконечно малой, если 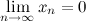
Последовательность 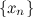 называется бесконечно большой, если для любого
называется бесконечно большой, если для любого 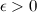 существует номер
существует номер 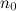 такое, что для любого
такое, что для любого 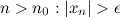
Теорема:
Пусть 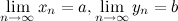 , тогда
, тогда
а) 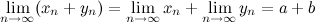 ;
;
б) 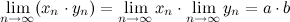 ;
;
в) если 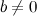 , то начиная с некоторого номера заданная последовательность
, то начиная с некоторого номера заданная последовательность