Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.
Итак, если уравнения двух непараллельных плоскостей -- 
и 
, то прямая, являющаяся их линией пересечения, задается системой уравнений
 |
И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.
Канонические уравнения прямой в пространстве
Если известна некоторая точка пространства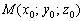 
, принадлежащая прямой, и направляющий вектор 
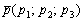данной прямой, то канонические уравнения этой прямой выражаются формулами:
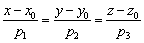
Координаты направляющего вектора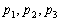 
не равны нулю.
Пример 1
Составить канонические уравнения прямой по точке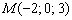 
и направляющему вектору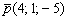 
Решение: Канонические уравнения прямой составим по формуле: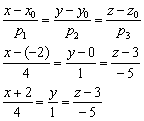
Ответ: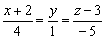 
В ряде задач требуется найти какую-нибудь другую точку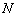 
, принадлежащую данной прямой. Как это сделать?
Берём полученные уравнения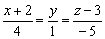 
и мысленно «отщипываем», например, левый кусочек: 
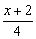. Теперь этот кусочек приравниваем к любому числу (помним, что ноль уже был), например, к единице: 
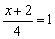. Так как 
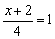, то и два других «куска» тоже должны быть равны единице. По сути, нужно решить систему: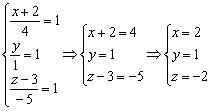
Выполним чертёж в прямоугольной системе координат. Заодно вспомним, как правильно откладывать точки в пространстве:
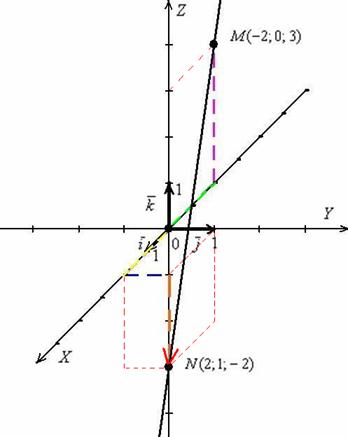
Строим точку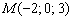 
:
– от начала координат в отрицательном направлении оси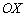 
откладываем отрезок первой координаты 
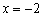(зелёный пунктир);
– вторая координата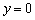 
нулевая, поэтому «не дёргаемся» с оси 
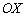ни влево, ни вправо;
– в соответствие с третьей координатой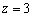 
отмеряем три единицы вверх (фиолетовый пунктир).
Строим точку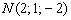 
: отмеряем две единицы «на себя» (желтый пунктир), одну единицу вправо (синий пунктир) и две единицы вниз (коричневый пунктир). Коричневый пунктир и сама точка 
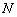наложились на координатную ось, обратите внимание, что они находятся в нижнем полупространстве и ПЕРЕД осью 
.
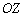Сама прямая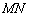 
проходит над осью 
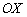и, если меня не подводит глазомер, над осью 
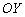. Не подводит, убедился аналитически. Если бы прямая 
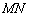проходила ЗА осью 
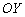, то следовало бы стереть ластиком частичку линии 
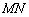сверху и снизу точки скрещивания.
У прямой бесконечно много направляющих векторов, например: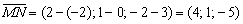
(красная стрелка)
Получился в точности исходный вектор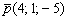 
, но это чистая случайность, такую уж я выбрал точку 
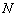. Все направляющие векторы прямой коллинеарны, и их соответствующие координаты пропорциональны
