Угол между двумя прямыми (на плоскости)
Пусть две неперпендикулярные прямые A1, A2 (взятые в данном порядке) представляются уравнениями
y=a1x+b1
y=a2x+b2
Тогда формула 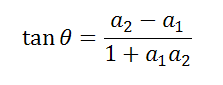
Даёт угол, на который надо повернуть первую прямую, чтобы она стала параллельно второй.
Замечание 1.
Если хотя бы одна из прямых A1, A2 параллельно оси OY, то выше написанная формула неприменима. В этом случае угол θ определяется следующим образом:
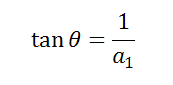
2. Когда прямая A1 параллельно оси OY, а A2 не параллельна, применяем формулу 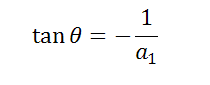
3. Когда обе прямая параллельно оси OY, они и параллельны и между собой, так что 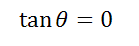
Замечание 2.
Угол между прямыми, заданными уравнениями
A1 x+B1 y+C1=0 и A2 x+B2 y+C2=0
Можно найти по формуле 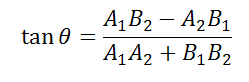
При A1A2+B1B2=0, то угол θ=±90
Если прямые перпендикулярны (θ=±90), то выражение 1+a1a2, стоящее в знаменателе, обращается в нуль, тогда θ надо считать равным ±90
а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
Это условие может быть записано также в виде
k1k2 = -1.
б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства
A1A2 + B1B2 = 0

