Угол наклона прямой к оси Ox в фиксированной прямоугольной декартовой системе координат Oxy на плоскости - это угол, отсчитываемый от положительного направления оси Ох до прямой против хода часовой стрелки.

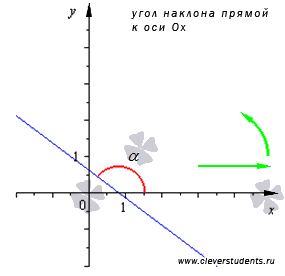
Если прямая параллельна оси абсцисс или совпадает с ней, то угол ее наклона считают равным нулю. Таким образом, угол наклона прямой  может принимать значения из интервала .

Угловым коэффициентом прямой называется тангенс угла наклона этой прямой.

Угловой коэффициент прямой обычно обозначают буквой k. Тогда по определению .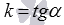

Положительный угловой коэффициент прямой указывает на возрастание ее графика функции, отрицательный угловой коэффициент – на убывание. Этой теме посвящена статья нахождение промежутков возрастания и убывания функции.

На рисунке показан угол наклона прямой и указано значение углового коэффициента при различных вариантах расположения прямой относительно прямоугольной системы координат.

Уравнение прямой, проходящей через данную точку в данном направлении

Предположим, что прямая проходит через точку M₁ (x₁,y₁) и образует с осью OX угол j. Составим уравнение этой прямой.

Y

 Будем искать уравнение прямой в виде уравнения с угловым коэффициентом: y = k · x + b. Угловой коэффициент прямой можно найти, зная угол наклона k = tg j. Возьмем произвольную точку M (x, y), лежащую на этой прямой, и найдем уравнение, связывающее переменные x и y. Так как точки М и M₁ лежат на прямой, то их координаты удовлетворяют уравнению прямой:

y = k · x + b,

y₁ = k · x₁ + b.

Вычитая эти равенства, получим:

y - y₁ = k · (x - x₁) - уравнение прямой, проходящей через данную точку в данном направлении.

Уравнение прямой, проходящей через две данные точки

Пусть даны точки A(x₁;y₁) и B(x₂;y₂). Уравнение прямой, проходящей через точки A(x₁;y₁) и B(x₂;y₂) имеет вид:

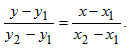
Решение: Подставляя в уравнение (8) x₁=1, y₁=2, x₂=-1; y₂=1 получим: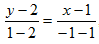 
 откуда  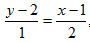или 2у-4=х-1, или окончательно х-2у+3=0