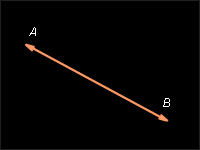
Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом.
На рисунках направление вектора обозначается стрелкой от начала к концу. Если длина рассматриваемого отрезка равна нулю, то есть отрезок вырождается в точку, то эта точка тоже может рассматриваться как вектор. Такой вектор называется нулевым и имеет произвольное направление.
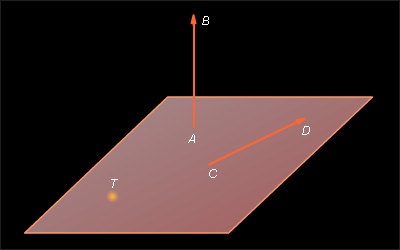
На изображены ненулевые векторы 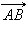 и
и 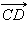 и нулевой вектор
и нулевой вектор 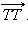 Нулевой вектор иногда обозначается символом
Нулевой вектор иногда обозначается символом 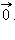
Длиной (модулем) ненулевого вектора 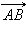 называется длина отрезка AB. Она обозначается как
называется длина отрезка AB. Она обозначается как 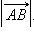 Длина нулевого вектора равна нулю:
Длина нулевого вектора равна нулю: 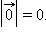
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Поскольку нулевой вектор может иметь произвольное направление, то разумно считать его коллинеарным любому ненулевому вектору.
Если два ненулевых вектора 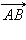 и
и 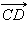 коллинеарны, а лучи AB и CD сонаправлены, то векторы
коллинеарны, а лучи AB и CD сонаправлены, то векторы  и
и  называются сонаправленными. Этот факт обозначается так:
называются сонаправленными. Этот факт обозначается так: 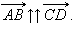 Если же эти лучи не являются сонаправленными, то векторы
Если же эти лучи не являются сонаправленными, то векторы 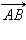 и
и 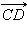 называются противонаправленными. Этот факт обозначается так:
называются противонаправленными. Этот факт обозначается так: 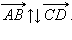
1.Равные вектора
Два вектора называются равными, если они сонаправлены и их длины равны
2.Два вектора называются противоположными, если их длины равны, и они противоположно направлены
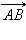 и
и 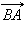 – противоположные векторы.
– противоположные векторы.
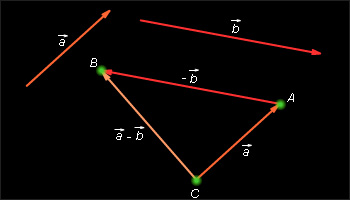
3.Суммой двух векторов 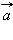 и
и 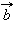 называется новый вектор
называется новый вектор 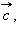 который обозначается
который обозначается 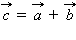 и получается следующим образом.
и получается следующим образом.
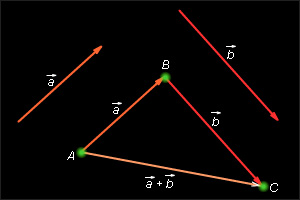
Отложим от произвольной точки A вектор 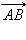 , равный
, равный 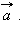 Теперь от точки B отложим вектор
Теперь от точки B отложим вектор 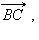 равный
равный 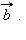 Вектор
Вектор  и называется суммой векторов
и называется суммой векторов 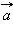 и
и 
 Это правило сложения векторов называется правилом треугольника.
Это правило сложения векторов называется правилом треугольника.
Для сложения двух неколлинеарных векторов можно воспользоваться правилом параллелограмма.
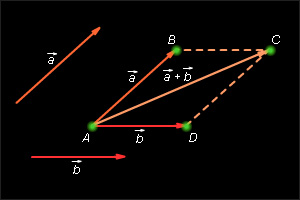
Для любых векторов 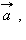
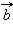 и
и 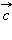 справедливы равенства:
справедливы равенства:
-
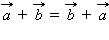 (переместительный закон);
(переместительный закон); -
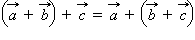 (сочетательный закон).
(сочетательный закон).
Разностью векторов 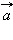 и
и 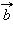 называется такой вектор
называется такой вектор 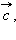 сумма которого с вектором
сумма которого с вектором 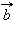 равна вектору
равна вектору 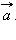 Обозначается разность векторов так:
Обозначается разность векторов так: 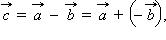 где
где  – вектор, противоположный вектору
– вектор, противоположный вектору 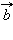 .
.
Направляющие косинуса
Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.
Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.
Сумма квадратов направляющих косинусов равна единице.
Формулы вычисления направляющих косинусов вектора
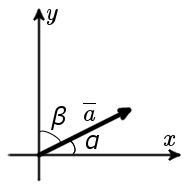
1.Формула вычисления направляющих косинусов вектора для плоских задач
В случае плоской задачи направляющие косинусы вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой
| cos α = | ax | ; | cos β = | ay |
| |a| | |a| |
Свойство:
2 α + cos2 β = 1
 |
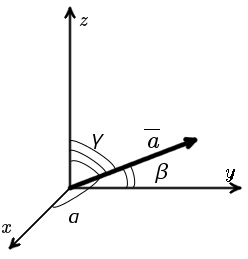
2.Формула вычисления направляющих косинусов вектора для пространственных задач
В случае пространственной задачи направляющие косинусы вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой
| cos α = | ax | ; | cos β = | ay | ; | cos γ = | az |
| |a| | |a| | |a| |
Свойство:
cos2 α + cos2 β + cos2 γ = 1
 |

