Ранг матрицы
Ранг матрицы – это максимальное количество линейно независимых строк. Или: ранг матрицы – это максимальное количество линейно независимых столбцов. Да, их количество всегда совпадает.
Сойство ранга матрицы:
1. Ранг матрицы равен нулю только для нулевой матрицы. В других случаях ранг матрицы равен некоторому положительном числу.
2. Ранг прямоугольной матрицы не превышает меньшего из двух чисел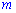 
и 
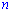т.е. 
.
3. Для квадратной матрицы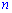 
-го порядка 
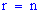только тогда, когда матрица невырожденная.
Невырожденная матрица (иначе неособенная матрица) ― квадратная матрица, определитель которой отличен от нуля. В противном случае матрица называется вырожденной.
4. В случае квадратной матрицы если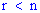 
то определитель матрицы равен нулю.
r-ранг-rank
n-порядок матрицы
Преобразования матрицы, не изменяющие ее ранг
Рассмотрим следующие элементарные преобразования матриц:
- Перестановка строк или столбцов.
- Умножение строки или столбца на ненулевое число.
- Прибавление к строке (столбцу) другой строки (столбца), предварительно умноженной на любое число.
Теорема. Элементарные преобразования не изменяют ранг матрицы.
Для доказательства теоремы достаточно убедиться в том, что в результате элементарных преобразований нулевой определитель остается нулевым, а ненулевой – ненулевым.
- Перестановка строк или столбцов матрицы изменяет только знак определителя.
- При умножении строки (столбца) матрицы на ненулевое число определитель умножается на это число.
- Определитель не изменяется, если к строке (столбцу) прибавляется другая строка (столбец).
