Обратная матрица
Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:
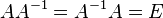
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Свойства обратной матрицы:
 , где
, где  обозначает определитель.
обозначает определитель.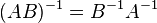 для любых двух обратимых матриц
для любых двух обратимых матриц  и
и  .
. где
где  обозначает транспонированную матрицу.
обозначает транспонированную матрицу. для любого коэффициента
для любого коэффициента  .
.- Если необходимо решить систему линейных уравнений
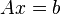 , (b — ненулевой вектор) где
, (b — ненулевой вектор) где  — искомый вектор, и если
— искомый вектор, и если 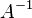 существует, то
существует, то  . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Способы нахождения обратной матрицы:
Начнем с самого ужасного и непонятного. Рассмотрим квадратную матрицу 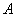 . Обратную матрицу
. Обратную матрицу 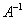 можно найти по следующей формуле:
можно найти по следующей формуле:
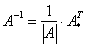 , где
, где 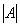 – определитель матрицы
– определитель матрицы 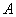 ,
, 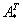 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 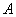 .
.
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Обозначения: Как вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом 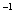
Пример:
Найти обратную матрицу для матрицы 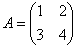
Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
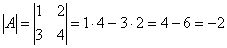
Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось, 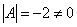 , а значит, всё в порядке.
, а значит, всё в порядке.
2) Находим матрицу миноров 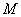 .
.
Матрица миноров имеет такие же размеры, как и матрица 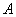 , то есть в данном случае
, то есть в данном случае 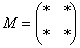 .
.
Возвращаемся к нашей матрице 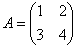
Сначала рассмотрим левый верхний элемент: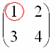
Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент: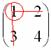
Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров: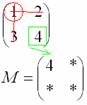
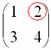
Рассматриваем следующий элемент матрицы 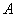 :
:
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент: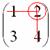
То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу: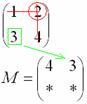
Аналогично рассматриваем элементы второй строки и находим их миноры: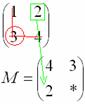
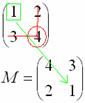
Готово.
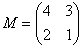 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы 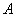 .
.
3) Находим матрицу алгебраических дополнений 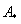 .
.
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: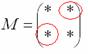
Именно у этих чисел, которые я обвел в кружок!
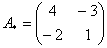 – матрица алгебраических дополнений соответствующих элементов матрицы
– матрица алгебраических дополнений соответствующих элементов матрицы 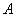 .
.
4) Находим транспонированную матрицу алгебраических дополнений 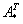 .
.
Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.
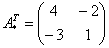 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 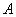 .
.
5) Ответ.
Вспоминаем нашу формулу 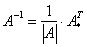
Всё найдено!
Таким образом, обратная матрица: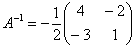
Необходимое и достаточное условие существования обратной матрицы
Исходная матрица должна иметь определитель, не равный 0.

