Матрицы. Виды матриц. Операции над матрицами

Определение:

Матрицей размера 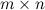 называется прямоугольная таблица специального вида, состоящая из  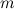строк и  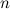столбцов, заполненная некоторыми элементами.

Количество строк и столбцов матрицы задают ее размеры.

Обозначение: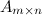 

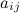Элементы матрицы  обозначаются , где 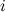 - номер строки, в которой находится элемент, а  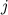- номер столбца.

Основные понятия матрицы:

Числа m и n называются порядками матрицы. В случае, если m=n, матрица называется квадратной, а число m=n — ее порядком.

В дальнейшем для записи матрицы будут применяться обозначение:

Впрочем, для краткого обозначения матрицы часто используется одна большая буква латинского алфавита, (например, А), либо символ ||aij||, а иногда и с разъяснением: A=||aij||=(aij) (i=1,2,…,m; j=1,2,…n)

Числа aij, входящие в состав данной матрицы, называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j — номер столбца.

Например, матрица:

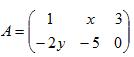
это матрица порядка 2×3, ее элементы a11=1, a12=x, a13=3, a21=-2y, …

Виды матриц:

Введем понятие матриц: квадратных, диагональных, единичных и нулевых.

1.Квадратная матрица

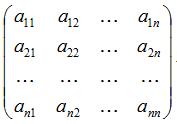
вводятся понятие главной и побочной диагоналей. Главной диагональю матрицы называется диагональ, идущая из левого верхнего угла матрицы в правый нижний ее угол.

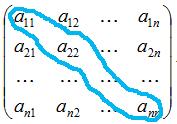
Побочной диагональю той же матрицы называется диагональ, идущая из левого нижнего угла в правый верхний угол.

2.Диагональная матрица

Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали равны нулю.

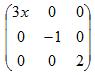
3.Понятие единочной матрицы

Единичной (обозначается Е иногда I) называется диагональная матрица с единицами на главной диагонали.

4.Нулевая матрица

Нулевой называется матрица, все элементы которой равны нулю.

5.Квадратная матрица

Две матрицы А и В называются равными (А=В), если они одинакового размера (т.е. имеют одинаковое количество строе и одинаковое количество столбцов и их соответствующие элементы равны). Так, если

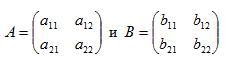
то А=B, если a11=b11, a12=b12, a21=b21, a22=b22

Действия над матрицами

1. Сложение матриц - поэлементная операция

2. Вычитание матриц - поэлементная операция

3. Произведение матрицы на число - поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

Пример:

5. Возведение в степень

m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'

Строки и столбцы поменялись местами

Пример: