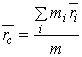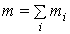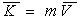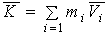Понятие центр масс.Закон движения центр масс.Импульс системы.Закон сохранения импульса.

ЦЕНТР МАСС

ЦЕНТР МАСС (центр инерции) системы материальных точек – условная (или эквивалентная) точка, представляющая собой одну из геометрических характеристик распределения масс в системе. Пусть 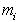 – масса 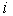-той (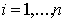) точки системы, а  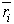– радиус-вектор этой точки в некоторой системе координат. Тогда радиус-вектор  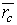точки С – центра масс определяется по формуле

 

 , 

Понятие центра масс широко используется в различных разделах механики. Например, центр масс тела можно принять в качестве центра тяжести – точки приложения суммарной силы однородного поля тяжести, действующего на тело.

Скорость центра масс, умноженная на суммарную массу системы, – это количество движения (импульс) этой системы.

Ускорение центра масс (по теореме о движении центра масс) определяется суммой внешних по отношению к системе сил, если считать их приложенными к некоторой эквивалентной материальной точке, которая помещена в центр масс и имеет массу .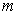

Количество движения (импульс) материальной точки – векторная динамическая мера 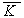ее движения, равная произведению массы 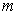этой точки на ее скорость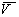 

Количество движения – одно из фундаментальных понятий механики. По второму закону Ньютона скорость изменения количества движения материальной точки равна силе, действующей на эту точку.

Количество движения системы материальных точек – геометрическая сумма количеств движения точек этой системы

Количество движения системы равно количеству движения эквивалентной материальной точки, масса которой равна сумме масс точек системы и которая помещена в центр С масс системы, т.к.

В применении к абсолютно твердому телу это позволяет считать количество движения тела динамической мерой его поступательного движения со скоростью центра масс.

Движение твердого тела может быть представлено в виде суперпозиции (сложения) двух движений: поступательного движения системы координат OXYZ с началом в некоторой точке О тела и вращательного движения тела вокруг точки О относительно системы OXYZ. Поэтому с точки зрения кинематики скорость каждой точки тела может быть принята в качестве характеристики «поступательного движения» тела. Однако с точки зрения динамики выбор точки С – центра масс тела –предпочтительней, т.к. именно с ее скоростью 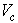 связано количество движения тела.

Пусть система будет неизменяемой. В этом случае ее называют абсолютно твердым телом или просто телом.

Уравнение движения твердого тела получим, сложив уравнения (16.1.1):

Рассмотрим левую часть уравнения. Следуя уравнению (15.2.1) можем записать:

Дважды продифференцировав по времени, найдем:

или

Левая часть найдена. В правой останется только сумма внешних сил, так как согласно (15.1.1) сумма внутренних сил равна нулю. Итак

Это аналитическое представление теоремы о движении центра масс системы.

Произведение суммарной массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил.

Проектируя уравнение (16.2.5) на оси координат, получим

то есть дифференциальные уравнения движения в проекциях. Значение теоремы о движении центра масс:

1. Решения, которые мы получаем, рассматривая данное тело как материальную точку, определяют закон движения центра масс этого тела.

2. Все внутренние силы можно исключить из рассмотрения.

 

 

Теорема о движении центра масс дает следующие следствия:

1. Если сумма действующих на систему внешних сил равна нулю

то центр масс системы движется равномерно и прямолинейно, то есть, при М = const:

2. Пусть , тогда

Если сумма проекций внешних сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная.

Эти два следствия выражают закон сохранения движения центра масс системы.

 Центром инерции, или центром масс, системы материальных точек называют такую точку С (рис. 3.2), радиус-вектор которой

где  – общая масса системы, n – число точек системы. 
       При этом не надо путать центр масс с центром тяжести системы – с точкой приложения равнодействующей сил тяжести всех тел системы. 
       Центр тяжести совпадает с центром масс (центром инерции), если g (ускорение силы тяжести) для всех тел системы одинаково (когда размеры системы гораздо меньше размеров Земли).

       Скорость центра инерции системы равна:

       Здесь

- импульс системы тел,  – скорость i-го тела системы. 
       Так как  , то импульс системы тел можно определить по формуле

– импульс системы тел равен произведению массы системы на скорость её центра инерции.

 

Закон сохранения импульса. Выясним, как изменяются импульсы двух тел при их взаимодействии.

Обозначим скорости тел массами m1 и m2 до взаимодействия через  и , а после взаимодействия — через  и .

По третьему закону Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому их можно обозначить  и .

Для изменений импульсов тел при их взаимодействии на основании равенства (16.2) можно записать

,

,

где t — время взаимодействия тел. Из этих выражений получаем

. (16.3)

Таким образом, векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия.

Экспериментальные исследования взаимодействий различных тел — от планет и звезд до атомов и элементарных частиц — показали, что в любой системе взаимодействующих между собой тел при отсутствии действия сил со стороны других тел, не входящих в систему, или равенстве нулю суммы действующих сил геометрическая сумма импульсов тел остается неизменной.

Система тел, не взаимодействующих с другими телами, не входящими в эту систему, называется замкнутой системой.

В замкнутой системе геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой.

Этот фундаментальный закон природы называется законом сохранения импульса.

Необходимым условием применимости закона сохранения импульса к системе взаимодействующих тел является использование инерциальной системы отсчета.