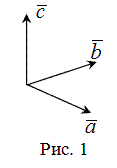
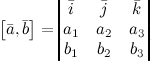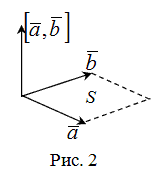Векторным произведением ненулевых векторов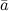 
и 
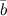называется вектор 
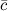, обозначаемый символом 
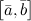или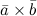 
, длина которого 
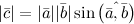(рис. 1).
Векторное произведение векторов.
Свойства векторного произведения:
1°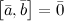 
, тогда и только тогда, когда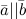 
2°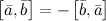 
3° Модуль векторного произведения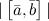 
равен площади параллелограмма, построенного на заданных векторах 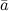и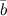 (рис. 2), т.е.
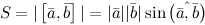
4°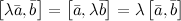 
5°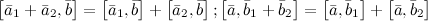 
Если векторы заданы своими координатами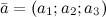 
, 
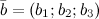, то векторное произведение находится по формуле:
