Вектором называется направленный отрезок AB¯=a¯.
Длиной или модулем вектора называется расстояние между его началом и концом. Записи |АВ| и |a| обозначают модули векторов АВ и a.
Два параллельных вектора - коллинеарны.
Нулевой вектор - начало и конец совпадают. Нулевой векор коллинеарен любому вектору.
Коллинеарные векторы:
1) сонаправлены
2) противоположнонаправлены
Если векторы совмещаются параллельным переносом, то они равны.
Коэффициент разложения вектора а и наз-ся его координатами в прямоугольной сист. координат: а(х; у)
Действия над векторами.
1. Умножение вектора на число.
(Произведением вектора a и числа α называется вектор, обозначаемый α∙a. (или наоборот a∙α), модуль которого равен |α a| =|α||a|, а направление совпадает с направлением вектора a, если α>0, и противоположно ему, если α< 0.
В координатах:
каждаяя координата вектора умножается на число;
если даны две точки, то вектор равен: из конца отнимаем начало соответсвующих координат.
длина (модуль) вектора = корень квадратный из суммы координат, каждая из которых взята в квадрате.
2. Сумма двух векторов:
правило треугольника и правило паралелограмма.
В координатах складываются соответсвующие координаты.
3. Разность векторов:
в координатах вычитание соответствующих координат.
Скалярное произведение векторов.
Скалярным произведением двух ненулевых векторов 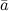 и
и 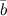 называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними:
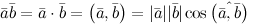
Если хотя бы один из векторов 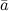 или
или 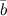 равен нулевому вектору, то
равен нулевому вектору, то 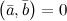 .
.
Свойства скалярного произведения:
1° 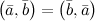 - симметричность.
- симметричность.
2° 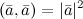 . Обозначается
. Обозначается 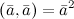 и называется скалярный квадрат.
и называется скалярный квадрат.
3° Если 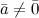 , то
, то 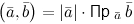
4° Если 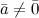 и
и 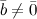 и
и 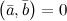 , то
, то  . Верно и обратное утверждение.
. Верно и обратное утверждение.
5° 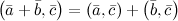
6° 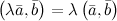
7° 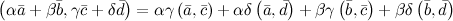
Если векторы 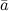 и
и 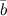 заданы своими координатами:
заданы своими координатами: 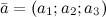 ,
, 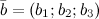 , то их скалярное произведение вычисляется по формуле:
, то их скалярное произведение вычисляется по формуле:
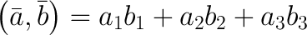
Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат.

