Обозначим через 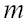 число появлений события
число появлений события 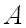 в
в 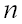 независимых испытаниях, в каждом из которых вероятность наступления этого события постоянна и равна
независимых испытаниях, в каждом из которых вероятность наступления этого события постоянна и равна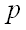 (соответственно вероятность непоявления также постоянна и равна
(соответственно вероятность непоявления также постоянна и равна 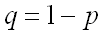 ).
).
Тогда, если 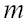 изменяется
изменяется 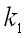 от до
от до 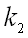 , то дробь
, то дробь 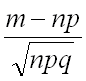 изменяется от
изменяется от 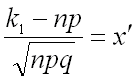 до
до 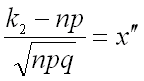 .
.
Следовательно, интегральную теорему Лапласа можно записать в виде:
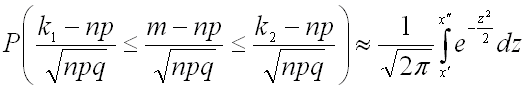
или
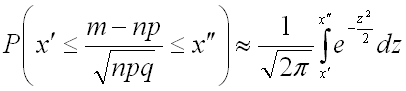 .
.
Теперь поставим задачу найти вероятность того, что отклонение относительной частоты 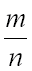 от постоянной вероятности
от постоянной вероятности 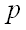 не превышает заданного числа
не превышает заданного числа 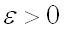 , то есть необходимо найти вероятность осуществления неравенства
, то есть необходимо найти вероятность осуществления неравенства
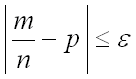 .
.
Преобразуем последнее неравенство, заменив знак модуля двойным неравенством и затем приведя к общему знаменателю:
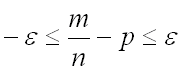 ,
,
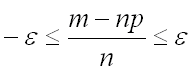 .
.
Умножим все неравенство на выражение 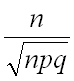 :
:
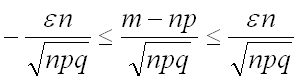 .
.
Теперь, если обозначить 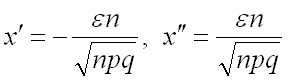 , то преобразованная теорема Лапласа может быть записана в виде:
, то преобразованная теорема Лапласа может быть записана в виде:
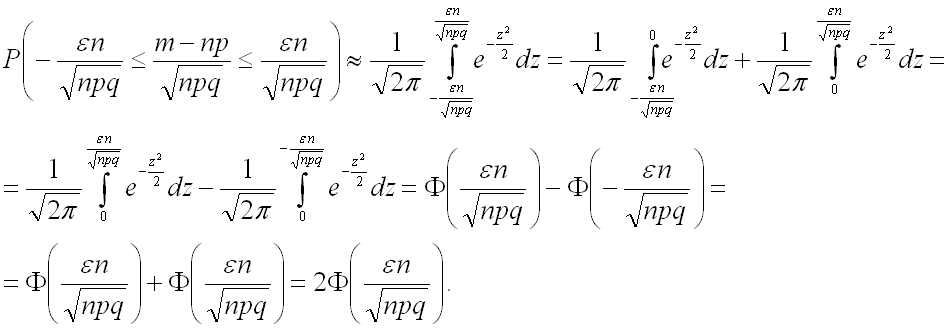
Заменив двойное неравенство в левой части последней формулы на исходное выражение 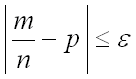 , окончательно получим:
, окончательно получим:
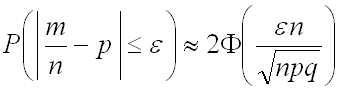 .
.
Вывод: вероятность того, что отклонение относительной частоты 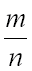 от постоянной вероятности
от постоянной вероятности 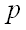 не превысит заданного числа
не превысит заданного числа 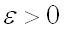 , приближенно равна удвоенной функции Лапласа с аргументом
, приближенно равна удвоенной функции Лапласа с аргументом 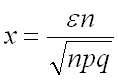 .
.
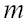 число появлений события
число появлений события 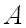 в
в 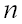 независимых испытаниях, в каждом из которых вероятность наступления этого события постоянна и равна
независимых испытаниях, в каждом из которых вероятность наступления этого события постоянна и равна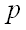 (соответственно вероятность непоявления также постоянна и равна
(соответственно вероятность непоявления также постоянна и равна 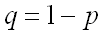 ).
).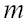 изменяется
изменяется 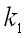 от до
от до 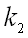 , то дробь
, то дробь 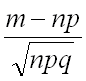 изменяется от
изменяется от 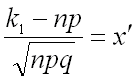 до
до 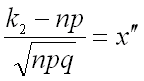 .
.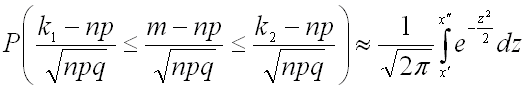
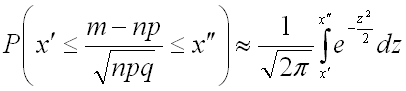 .
.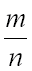 от постоянной вероятности
от постоянной вероятности 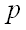 не превышает заданного числа
не превышает заданного числа 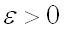 , то есть необходимо найти вероятность осуществления неравенства
, то есть необходимо найти вероятность осуществления неравенства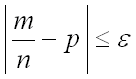 .
.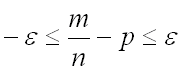 ,
,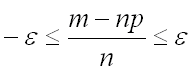 .
.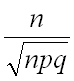 :
: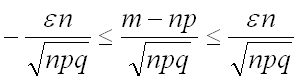 .
.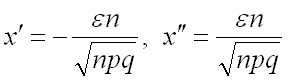 , то преобразованная теорема Лапласа может быть записана в виде:
, то преобразованная теорема Лапласа может быть записана в виде: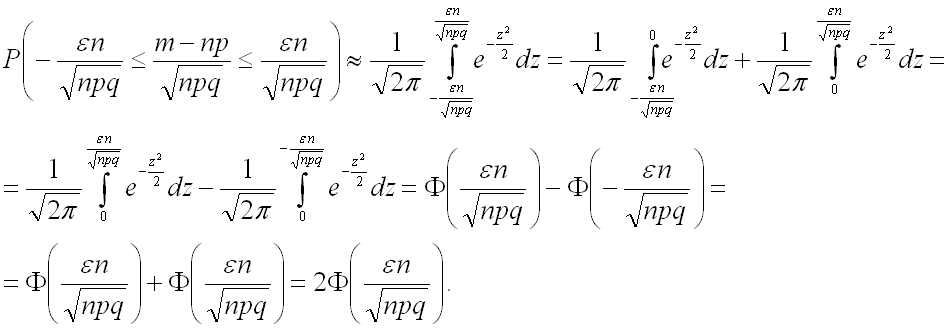
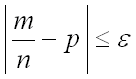 , окончательно получим:
, окончательно получим: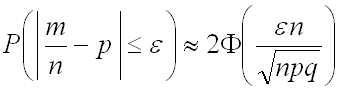 .
.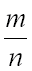 от постоянной вероятности
от постоянной вероятности 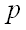 не превысит заданного числа
не превысит заданного числа 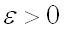 , приближенно равна удвоенной функции Лапласа с аргументом
, приближенно равна удвоенной функции Лапласа с аргументом 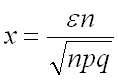 .
.
