Существует довольно много методов решения задач линейного программирования. Мы коснемся наиболее распространенных из этих методов и по возможности покажем границы их применимости. В данном параграфе описываются простейшие методы, пригодные в основном для решения задач с небольшим числом переменных. Однако, несмотря на простоту и наглядность, эти методы содержат в себе элементы подхода к решению класса задач, значительно более сложных, выходящих за пределы предположений, используемых в линейном программировании.
1). Графический метод. Если было указано, что в тех случаях, когда множество планов задачи линейного программирования образует выпуклый многогранник, линейная функция цели достигает своего оптимального значения в одной из вершин этого многогранника. Это свойство множества планов будет использовано для решения задачи линейного программирования.
2). Алгебраические методы. Поскольку с самого начала основная задача линейного программирования была сформулирована в виде системы m линейных уравнений с n неизвестными, то естественно обратить основное внимание на алгебраические методы решения задачи. При этом описанная выше в § 3 геометрическая интерпретация будет являться фактором, обеспечивающим ориентацию в направлении наиболее быстрого получения решения.
3). Метод последовательного улучшения плана (далее для краткости мы будем называть этот метод общепринятым названием симплексный метод) позволяет найти решение любой задачи линейного программирования, проделав ограниченное число шагов, каждый из которых является алгебраическим преобразованием, производимым и установленным правилам.Основная идея симплексного метода. Прежде всего для начала вычислений требуется, чтобы система уравнений (1.1) была приведена к такому виду, в котором какие-либо m неизвестных выражены через остальные n-m. Будем считать, что ранг матрицы А равен m (n>m). Предположим также, что свободные члены bi неотрицательны. В противном случае можно умножить правую и левую части уравнения, у которого свободный член отрицателен, на -1. Далее допустим, что неизвестные, которые выражены через остальные, есть x1, ..., xm. Таким образом, система (1.1) может быть записана в виде
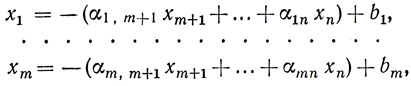
(1.7)
где b1≥0, ..., bm≥0 и коэффициенты α1,m+1, ..., αmn выражаются через a11, ..., amn. Неизвестные x1, ..., xm, которые находятся в левой части системы (1.7), образуют некоторый базис, поэтому эти неизвестные называются базисными. Остальные неизвестные являются небазисными (или свободными).
4) Симплекс-метод.Этот один из первых специализированных методов оптимизации, нацеленный на решение задач линейного программирования, в то время как методы простого и направленного перебора могут быть применены для решения практически любой задачи оптимизации. Он был предложен американцем Г. Данцигом в 1951 г. Симплекс-метод состоит в продвижении по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум

