16. Определение непрерывности на языке приращений. Исходя из определения докажите, что функция y = x3 + 2x2 непрерывна в т. х0=1.

   Непрерывность функции

Определение 1. Функция f(x) называется непрерывной в точке x₀, если .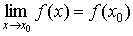

Более подробно это расшифровывается следующим образом:

1. .

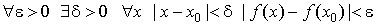2. 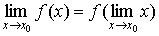. Другими словами, непрерывная функция характеризуется тем свойством, что можно менять местами знак функции и знак предела.

3. Обозначим 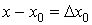 (приращение аргумента) и  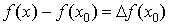 (приращение функции). Тогда непрерывная функция характеризуется тем свойством, что при  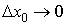 также и  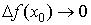, то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

         Определение 2. Функция f(x) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.