7. Понятие сложной функции. Понятие обратной функции. Примеры.

Сложная функция от х, то есть y = f [(x)], определённой для тех значений х, для которых значения j(х) входят в множество определения функции f (u). В таком случае говорят, что уявляется Сложная функция независимого аргумента х, а u -промежуточным аргументом. Например, если у = u², u = sinx, тоу = sin²х для всех значений х. Если же, например, у = 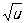, u =sinx, то у = 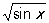, причём, если ограничиваться действительными значениями функции, Сложная функция укак функция х определена только для таких значений х, для которых sin ³ 0, то есть для 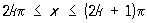, где k = 0, ± 1, ± 2,...

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.

Обратная функция функции $f$ обычно обозначается $f^{-1}$ , иногда также используется обозначение $f^{\mathrm{inv}}$ .

Функция $g:Y\to X$ является обратной к функции $f:X\to Y$ , если выполнены следующие тождества:

$f(g(y))=y$ для всех $y\in Y;$
$g(f(x))=x$ для всех $x\in X.$
Примеры[править | править исходный текст]
Если $F:\mathbb{R} \to \mathbb{R}_+,\; F(x) = a^x$ , где $a>0,$ то $F^{-1}(x) = \log_a x.$
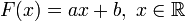Если $F(x) = ax+b, \; x\in \mathbb{R}$ , где $a,b\in \mathbb{R}$ фиксированные постоянные и $a \neq 0$ , то $F^{-1}(x) = \frac{x-b}{a}.$
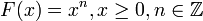Если $F(x)=x^n,x \ge 0, n\in \mathbb Z$ , то $F^{-1}(x)=\sqrt [n] {x}.$

7. Понятие сложной функции. Понятие обратной функции. Примеры.

Примеры[править | править исходный текст]