Покажем, что ускорение любой точки М плоской фигуры (так же, как и скорость) складывается из ускорений, которые точка получает при поступательном и вращательном движениях этой фигуры. Положение точки М по отношению к осям Оxy (см.рис.30) определяется радиусом-вектором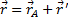 
где 
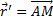. Тогда
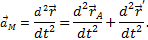
В правой части этого равенства первое слагаемое есть ускорение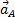 
полюса А, а второе слагаемое определяет ускорение 
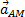, которое точка м получает при вращении фигуры вокруг полюса A. следовательно,
.
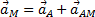Значение 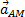, как ускорения точки вращающегося твердого тела, определяется как
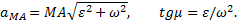
где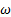 
и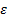 
- угловая скорость и угловое ускорение фигуры, а 
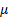- угол между вектором 
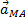и отрезком МА (рис.14).
Таким образом, ускорение любой точки М плоской фигуры геометрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление ускорения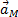 
, находятся построением соответствующего параллелограмма (рис.23).
Однако вычисление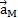 
с помощью параллелограмма, изображенного на рис.23, усложняет расчет, так как предварительно надо будет находить значение угла 
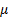, а затем - угла между векторам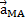и 
и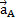 
, Поэтому при решении задач удобнее вектор 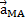заменять его касательной 
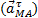и нормальной 
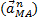составляющими и представить в виде
.
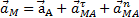При этом вектор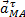 
направлен перпендикулярно АМ в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное; вектор 
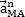всегда направлен от точки М к полюсу А (рис.15). Численно же
.
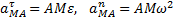Если полюс А движется не прямолинейно, то его ускорение можно тоже представить как сумму касательной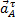 
и нормальной 
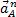составляющих, тогда
.
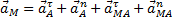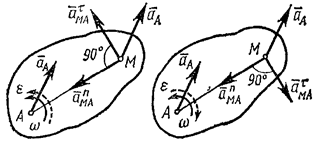
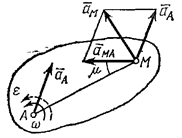
Рис.14 Рис.15
Наконец, когда точка М движется криволинейно и ее траектория известна, то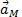 
можно заменить суммой 
.
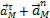