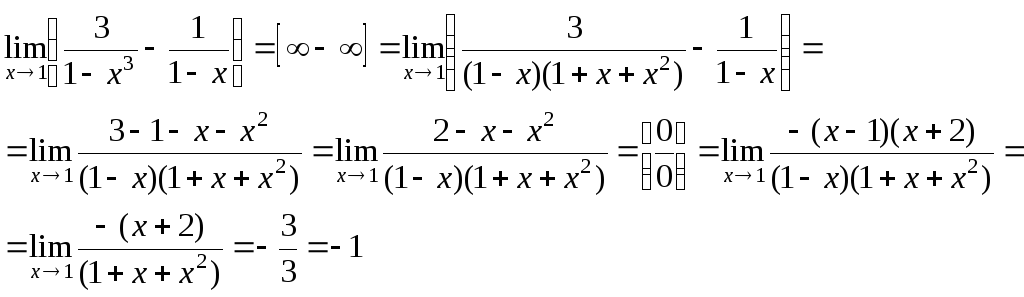Основные теоремы о пределах.

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

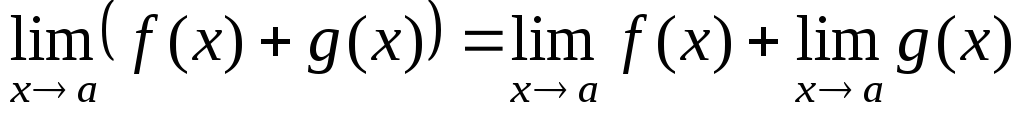
Пример. .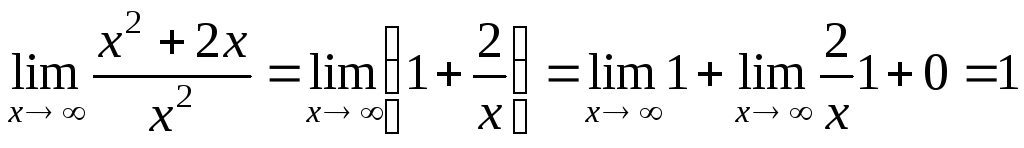

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

.

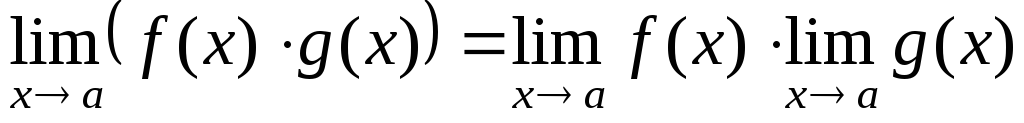Следствие 1. Постоянный множитель можно выносить за знак предела:

.

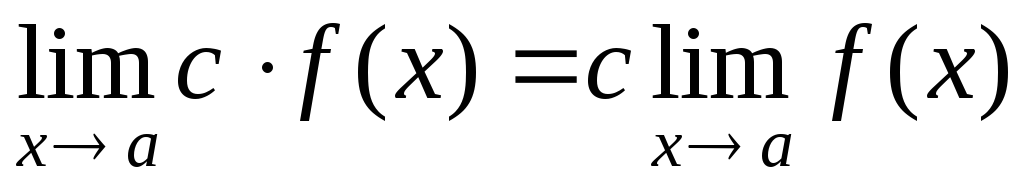Следствие 2. Предел степени равен степени предела:

.

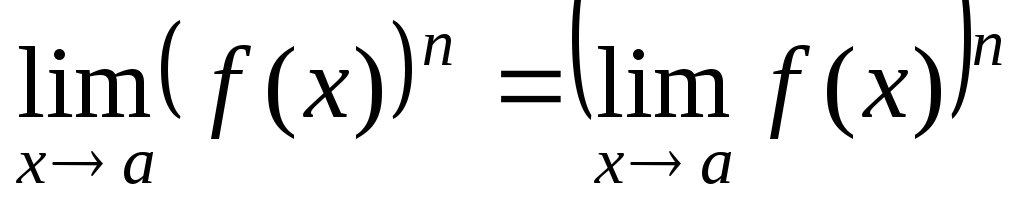Пример. .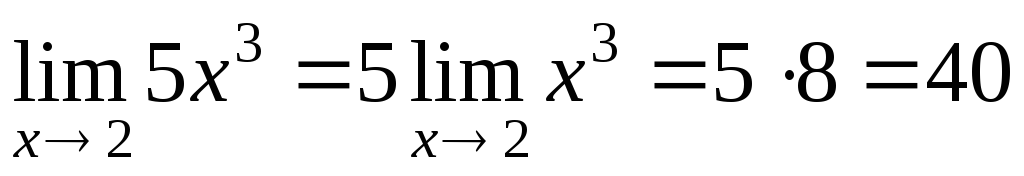

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

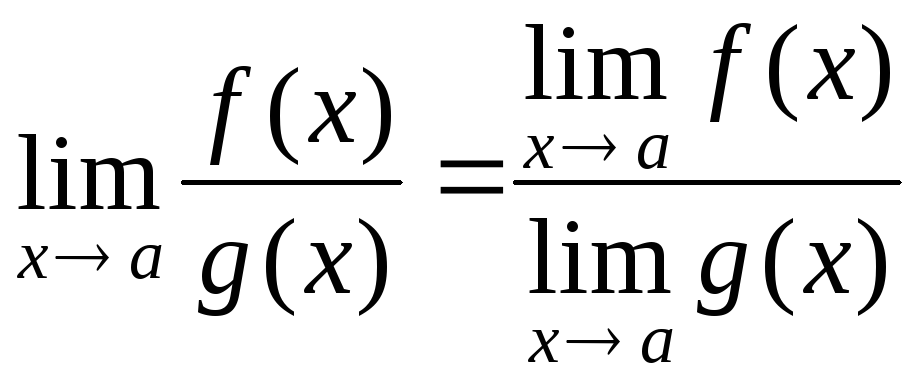, если .

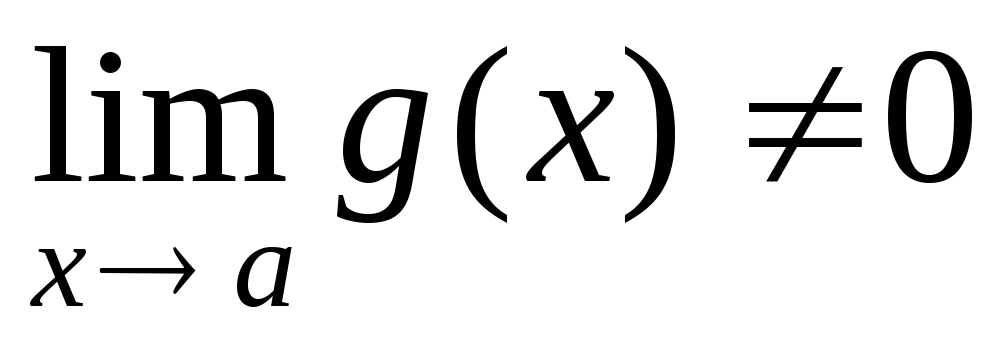Примеры.

1. .

2. .

3. 

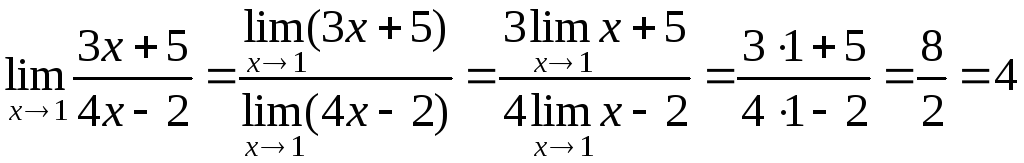
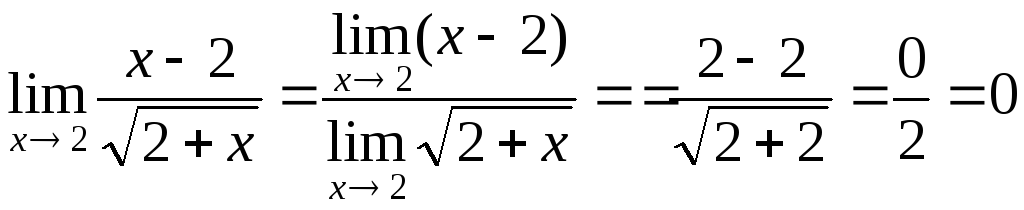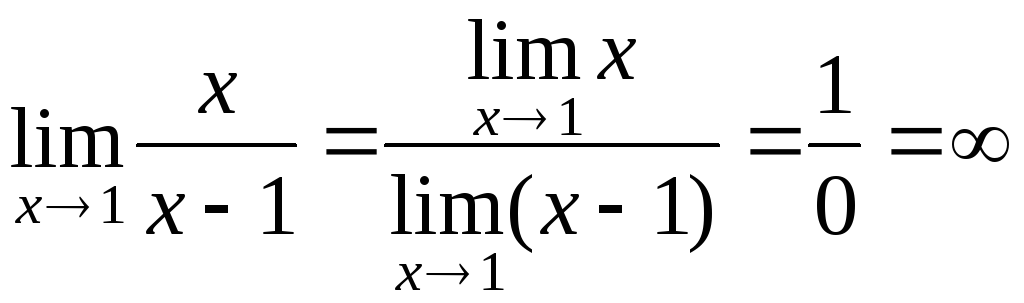
Типы неопределенностей и способы их раскрытия.

Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем.

Условные выражения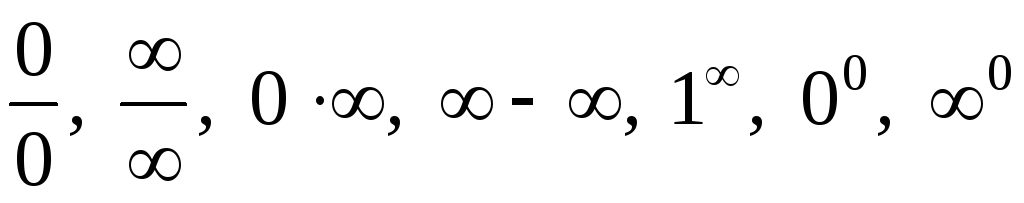 

характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов.

Рассмотрим некоторые приемы раскрытия неопределенностей.

I. Неопределенность .

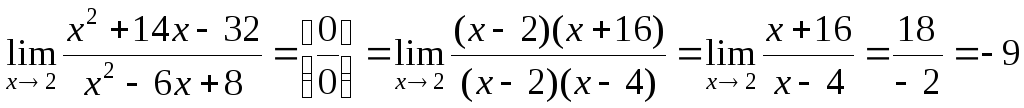1. Числитель и знаменатель разложили на множители. Общий множитель 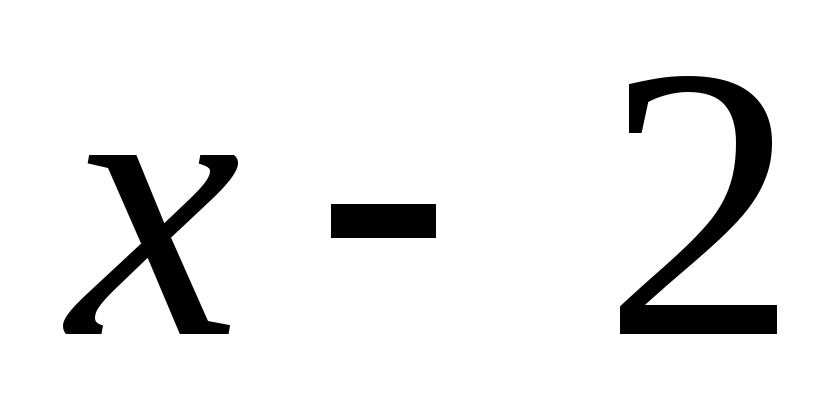сократили, т.о. ушли от неопределенности.

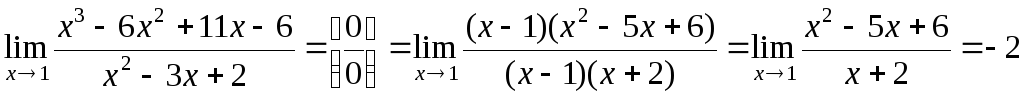2. При разложении числителя на множители воспользовались правилом деления многочлена на многочлен «углом». Так как число x=1 является корнем многочлена x³ – 6x² + 11x– 6, то при делении получим

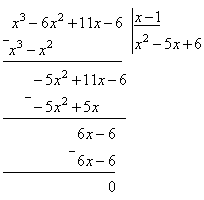
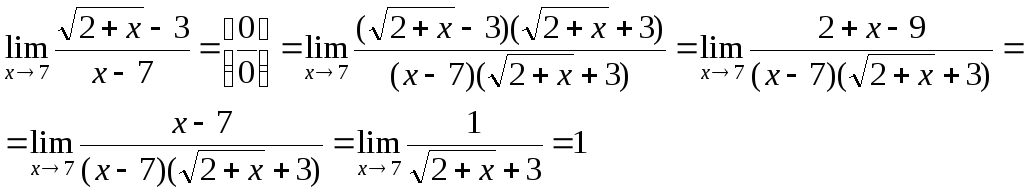3. Числитель и знаменатель умножили на выражение сопряженное числителю.

II. Неопределенность .

1. .

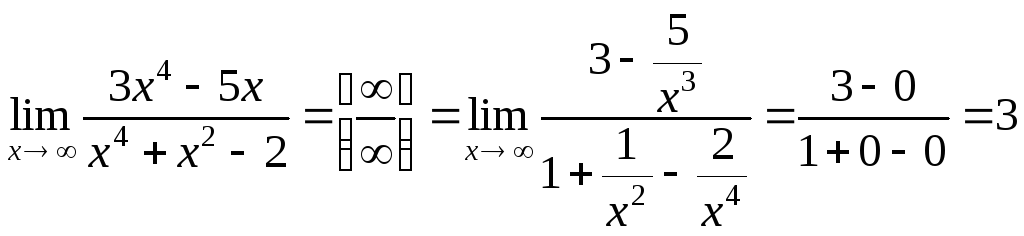При вычислении предела числитель и знаменатель данной дроби разделили на x в старшей степени.

2. .

3. 

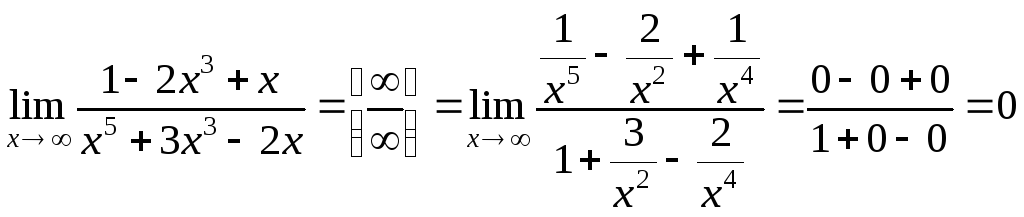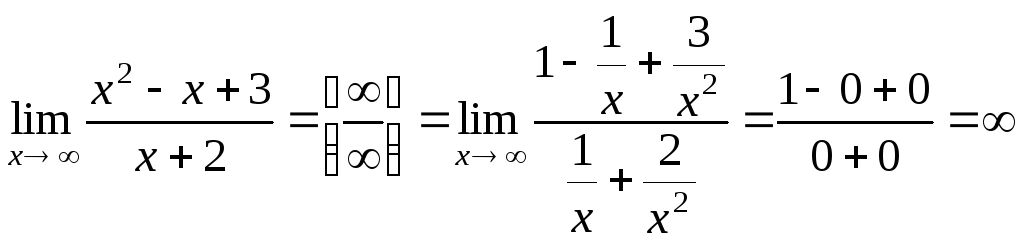
Следующие виды неопределенностей с помощью алгебраических преобразований функции, стоящей под знаком предела, сводят к одному из рассмотренных выше случаев  или .

III. Неопределенность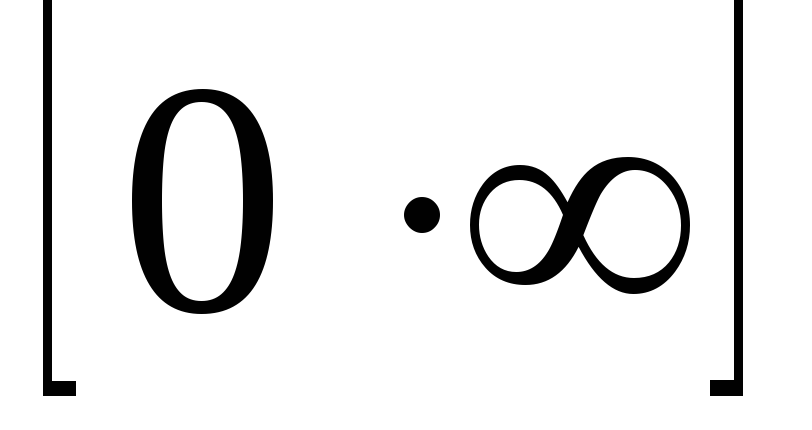  

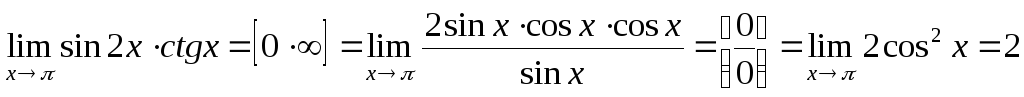
IV. Неопределенность ∞ –∞.