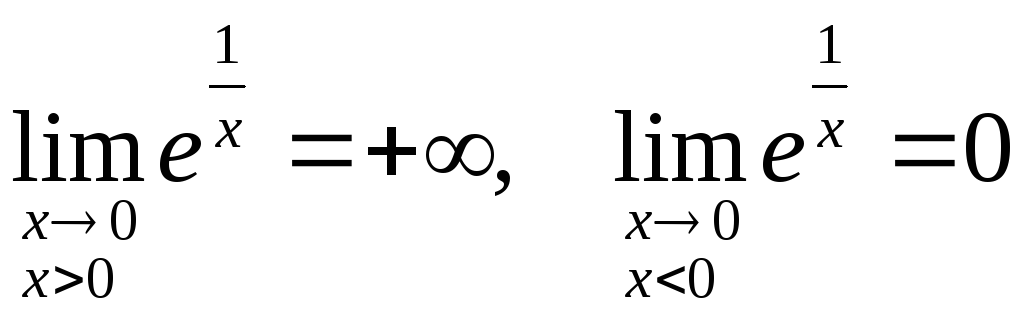Односторонние пределы
В определении предела функции предполагалось, что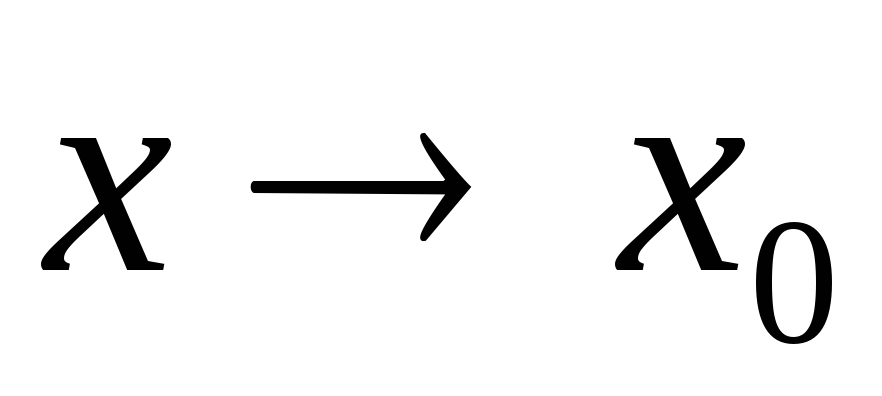 
произвольным образом. Если при вычислении предела функции
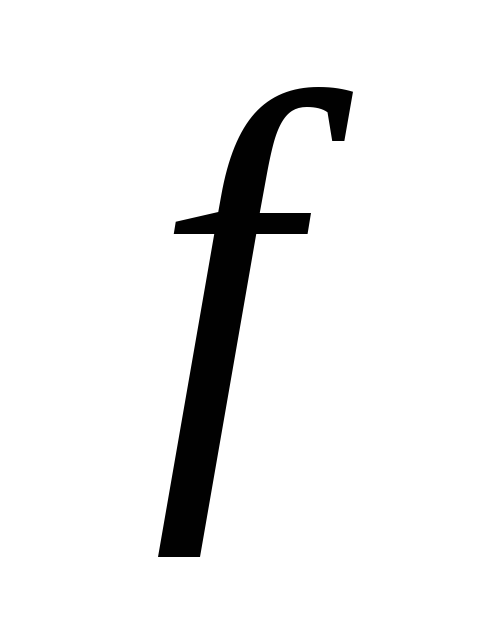при
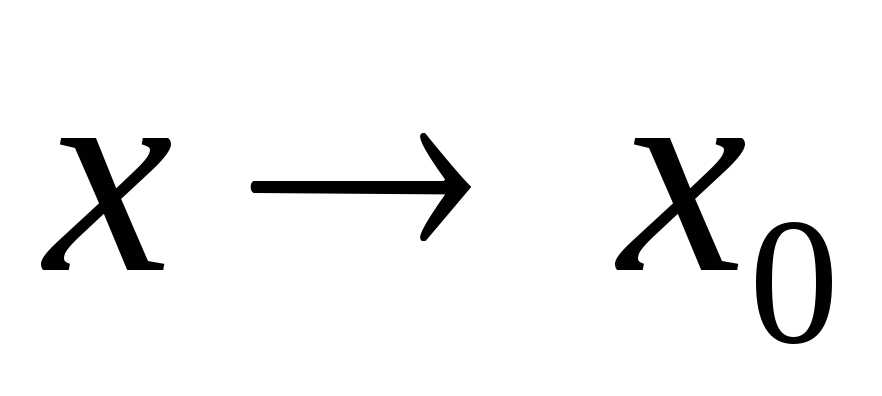считать, что
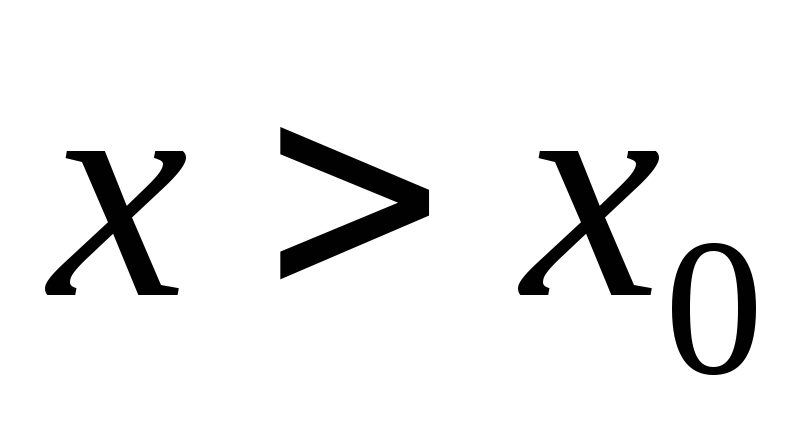, то получаютодносторонний предел справаилиправостороннийпредел функции в точке
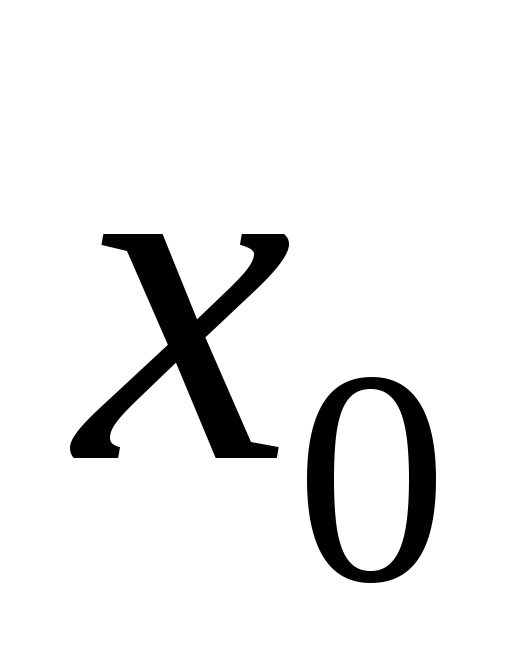. Если же считать, что
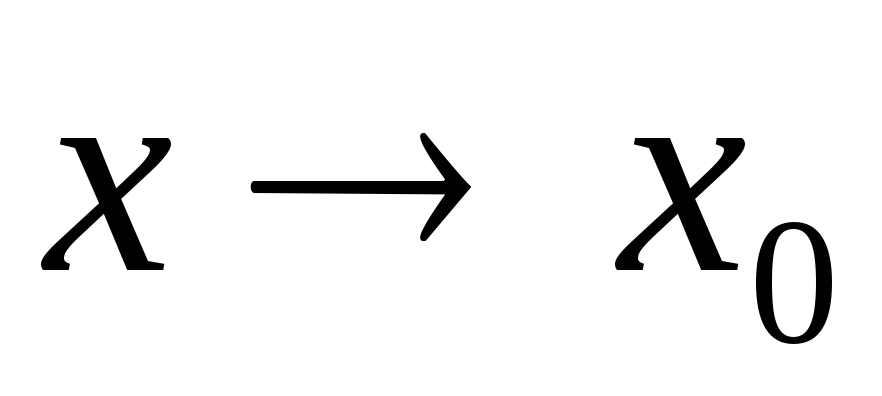и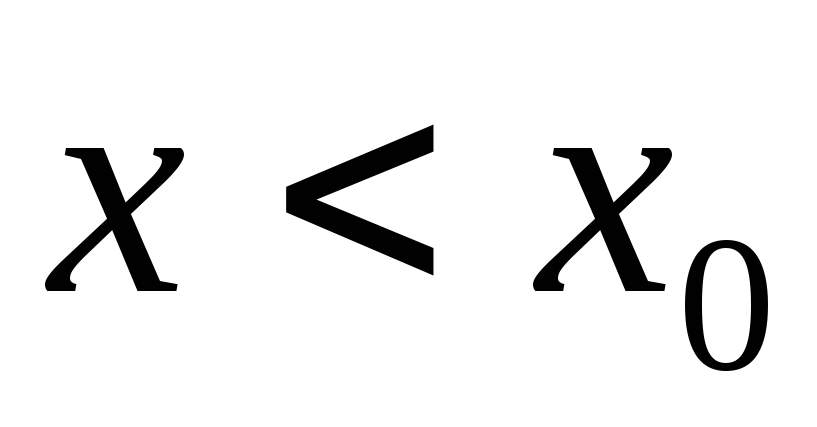
, то получают односторонний предел слеваилилевостороннийпредел.
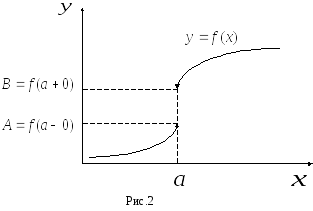
Так, например, односторонние пределы функции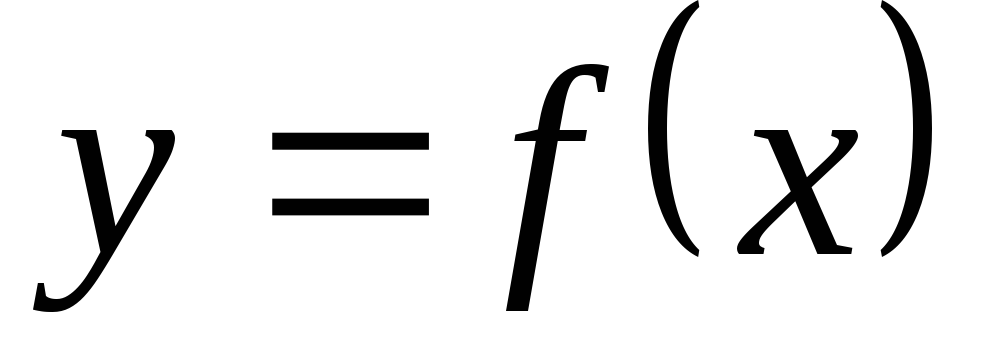 
, изображенной на Рис. 2, соответственно, равны:
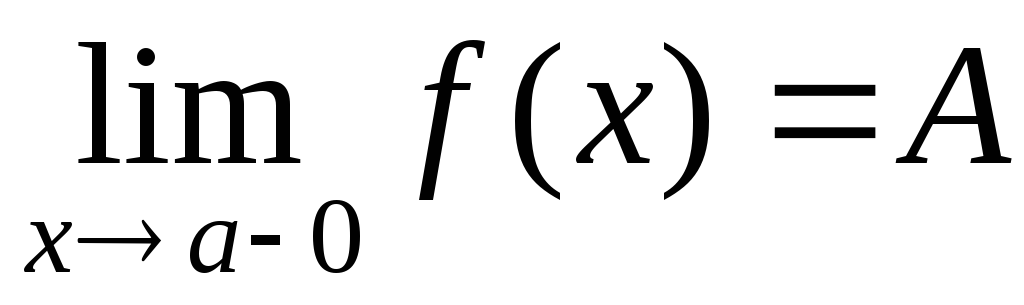и
.
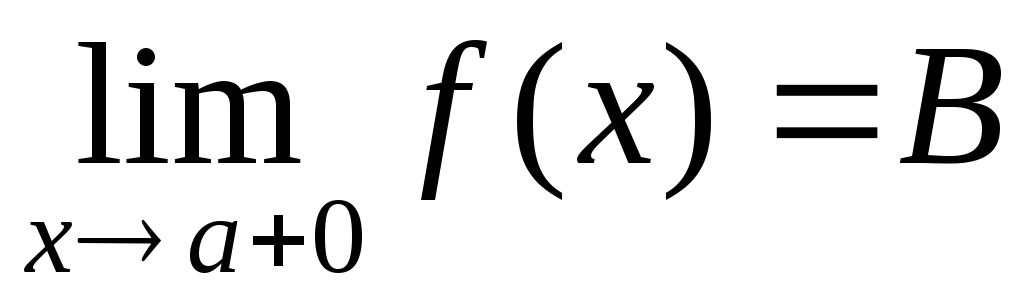Правосторонний предел обозначают символом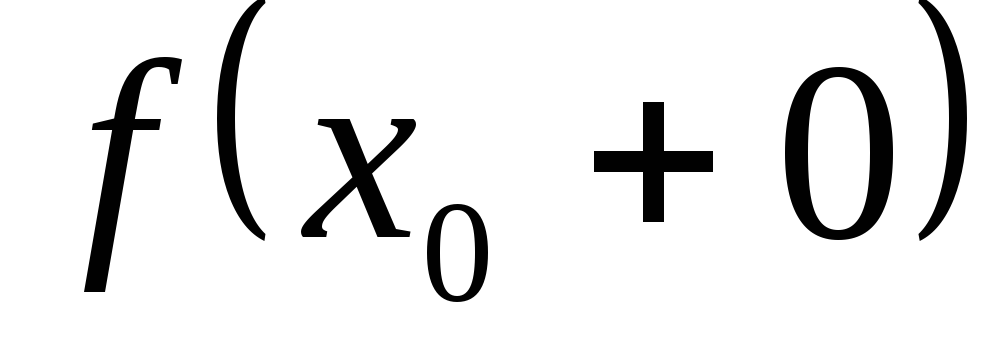 
, левосторонний ‑ символом
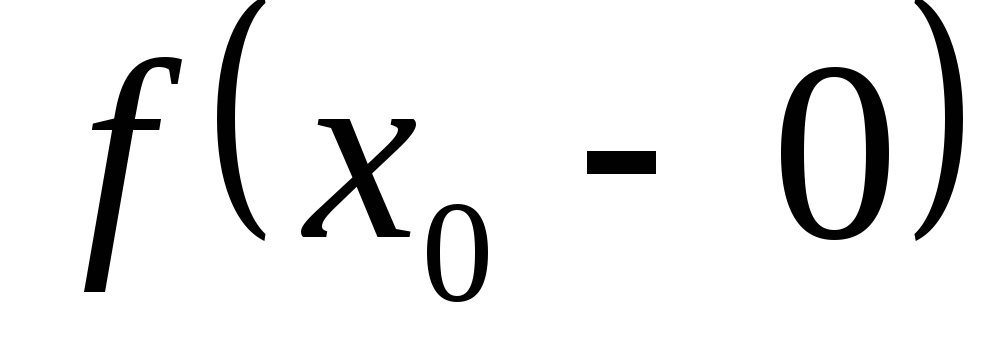. Таким образом:
.
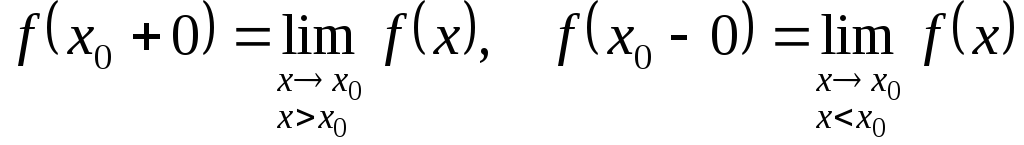В этих определениях предполагается, что функция определена на некотором промежутке соответственно справа или слева от точки сгущения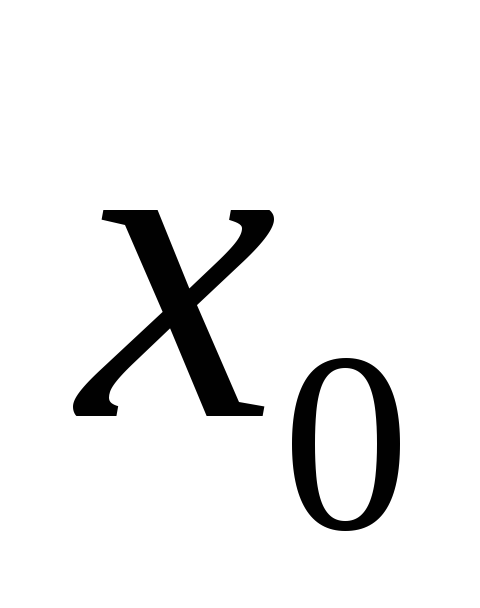 
.
Для того, чтобы у функции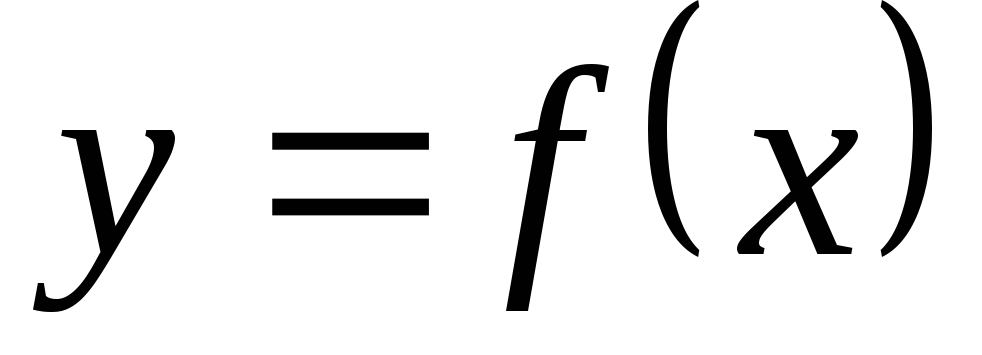 
в точке
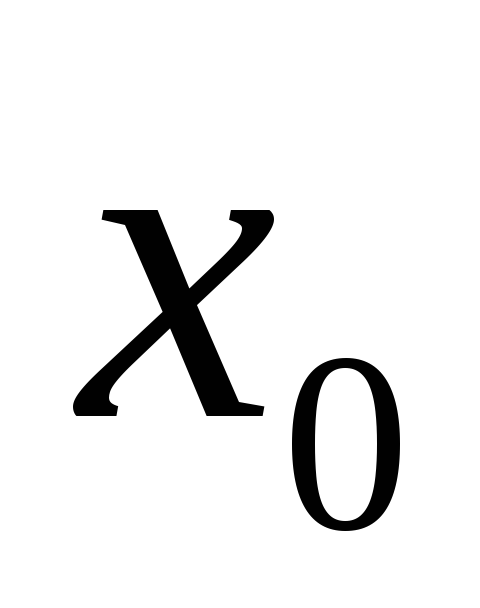существовал двусторонний предел
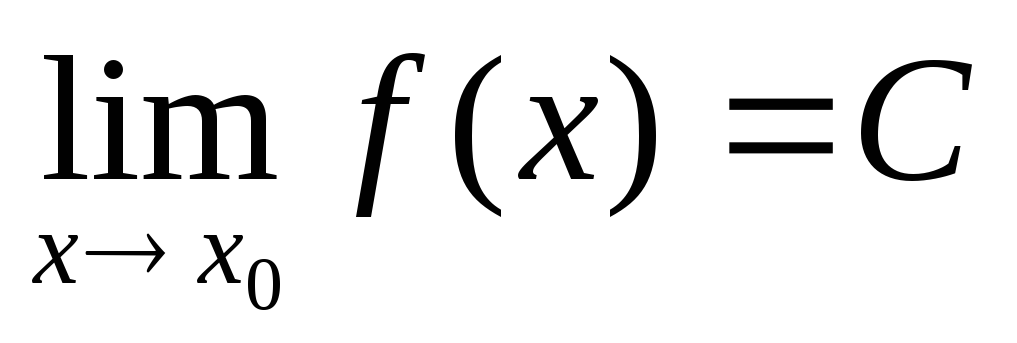, необходимо и достаточно, чтобы существовали левосторонний и правосторонний пределы
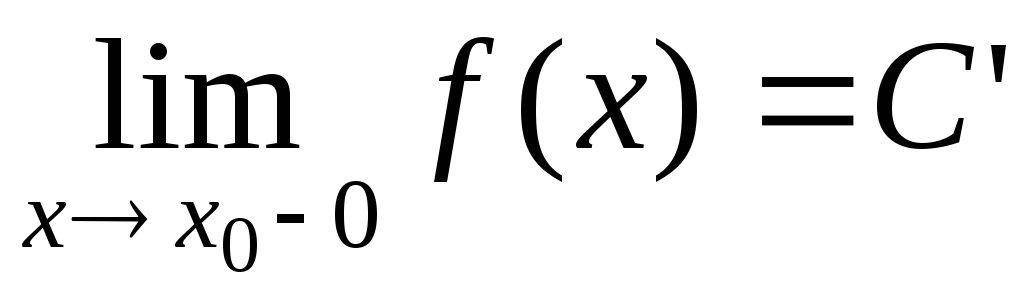и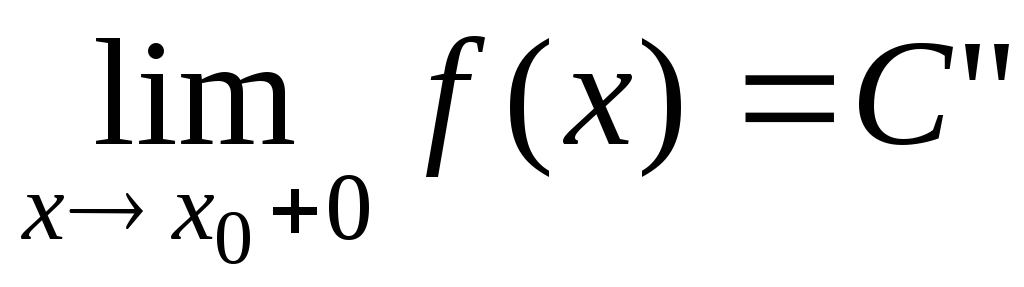
функции
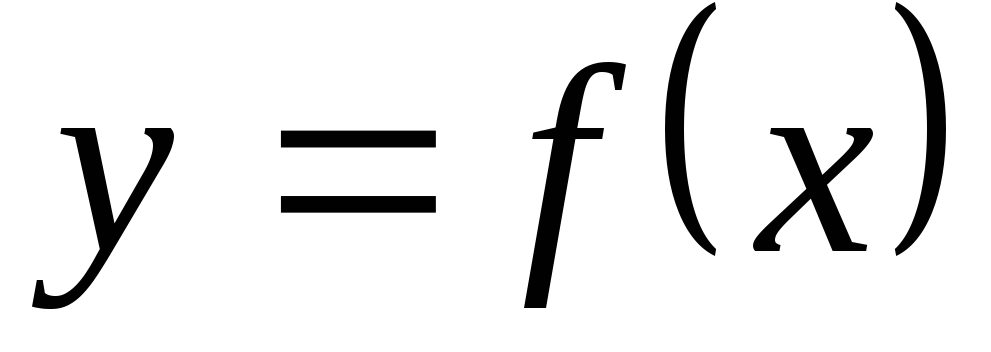в точке
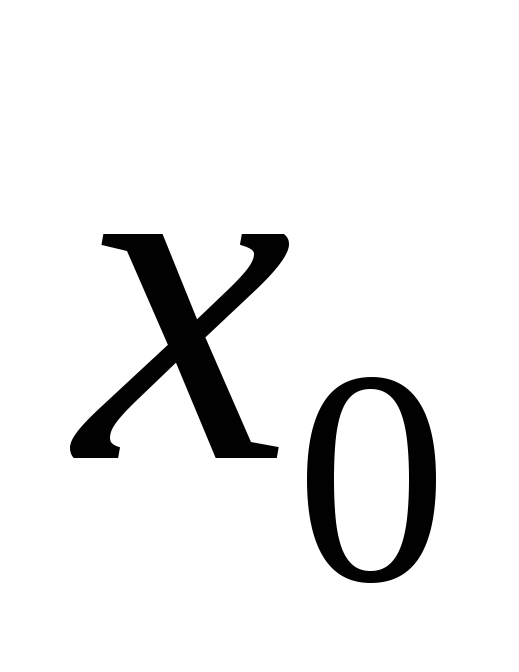, и эти пределы были равны между собой:
.
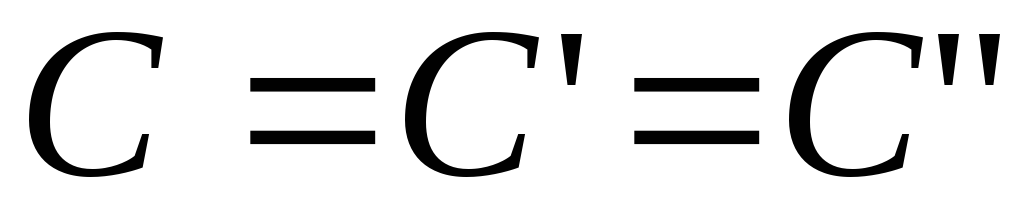Пример.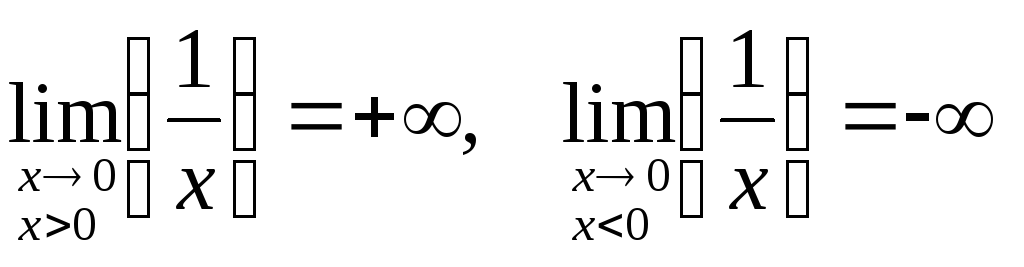
Пример.
