Понятие функции. Способы задания функции

Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут 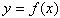, при этом x называют аргументом функции, y называют значением функции.

Существуют разные способы задания функций.

1. Аналитический способ.

Аналитический способ - это наиболее часто встречающийся способ задания функции.

Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например .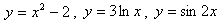

Рассмотрим первый пример - 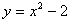. Здесь значению x = 1 соответствует 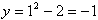, значению x = 3 соответствует  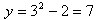и т. д.

Функция может быть задана на разных частях множества X разными функциями.

Например: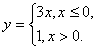



Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а слева формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.

Например 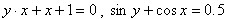. Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:

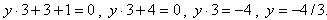. То есть, значение функции при х = 3 равно -4/3.



При аналитическом способе задания, функция может быть задана параметрически - это, когда х и у выражены через некоторый параметр t. Например,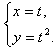



Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.



2. Графический способ.

При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом . Пример:



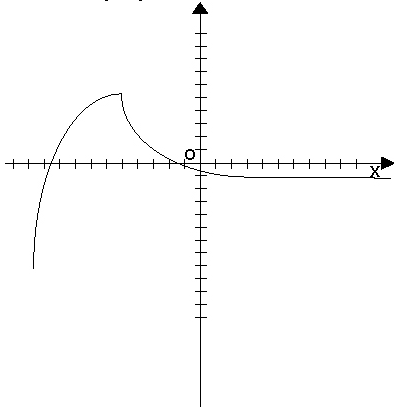
3. Словесный способ.

Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.

«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».



4. Табличный способ.

Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.

Пример:



Табличный способ задания функции очень удобен при обработке результатов исследований. Например, при выявлении зависимости между уровнем загрязнения окружающей среды и количеству людей, заболевших раком.

Область определения

Областью определения функции 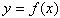 называется множество тех значений х, при которых функция определена. Иными словами, это те значения х, при которых функция «бывает».

Иногда область определения задается непосредственно уже при задании функции.

Например: 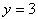 при 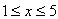. Здесь областью определения (ОДЗ) является промежуток [1;5]. При других значениях х функция не определена.

Однако, не всегда ОДЗ задана так непосредственно.



Чаще всего (для функций заданных аналитически), ОДЗ находят исходя из того, возможно ли при тех или иных значениях х произвести все операции, которые указаны в формуле.

Пример: ОДЗ функции 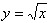 - промежуток [0;?). При всех других значениях х функция не определена (функции «не бывает»). Например, не существует действительного значения выражения .

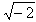При графическом изображении этой функции график будет находиться только в области допустимых значений, и ни на точку не выйдет за эти пределы.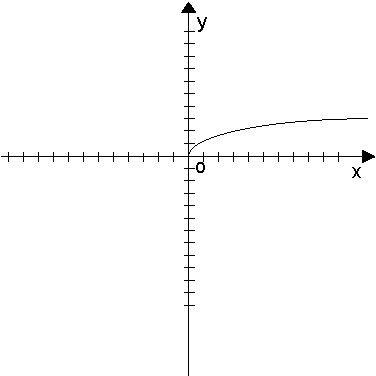



При табличном способе задания функции областью допустимых значений являются только те значения х, которые заданы в таблице.



Например:

Областью определения функции, заданной табличным способом –



является множество ОДЗ =   {3;5.1;10;12.5;13;20}



Пример1: Найти ОДЗ функции .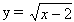

Квадратный корень можно извлечь только из положительных или равных 0 чисел, значит ОДЗ: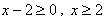 

Ответ: ОДЗ = [2;+?).

Пример 2: Найти ОДЗ функции .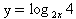

Основание логарифма должно быть положительным и отличным от 1.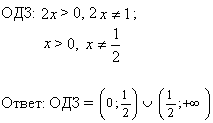
.

Множество значений функции

Множеством значений (область значений) функции 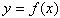 на заданной области определения Х, называется множество всех таких элементов у, для которых существует элемент

.

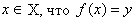Другими словами, область значений (ОЗ) - это множество всех возможных значений у.


Примеры:

Для функции: 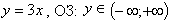, так для этой функции у может принимать любое действительное значение.

Для функции: 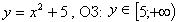, так для этой функции у может принимать значения только большие 5. Действительно,  всегда число положительное или равное 0, а к положительному числу или нулю прибавляем 5 - получаем число большее 5.

На следующих рисунках функции заданы графически.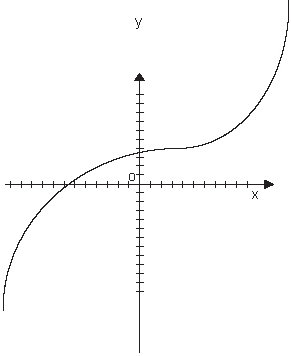



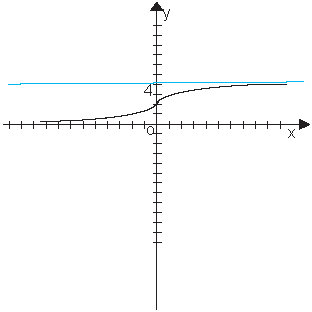
По графикам видно, что ОЗ первой функции – промежуток (-?;+?), а второй (0,4). 

Для следующей функции, заданной табличным способом –



область значений – это множество {9;23;90;110;112;300} 



Для функции Дирихле, заданной словесно «Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число», областью значений является множество, состоящее из двух чисел ОЗ = {0;1}..

Обратная функция

Пусть функция y = f(x) определена на множестве Х и имеет множество значений У.

О.4.1.Если каждому значению 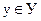 соответствует единственное значение  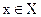, то определена функция  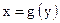с областью определения У и множеством значений Х. Такая функция 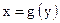называется обратнойк функции y = f(x).

Про функции y = f(x) и 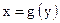 говорят, что они являются взаимно обратными.

Если использовать стандартные обозначения, то обратную функцию можно записать в виде

 .

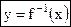Пример 5. Функци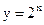и  и 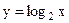 являются взаимно обратными.

Графики взаимно обратных функций y = f(x) и 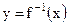 симметричны относительно биссектрисы I и III координатных углов.

Сложная функция (суперпозиция функций)

Пусть даны функции:

1) 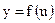 с областью определения U и множеством значений У;

2) 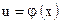 с областью определения Х и множеством значений  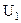, причем  .

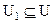О.4.2.Функция 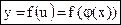 , заданная на множестве Х, называется сложной функцией от х или суперпозицией функци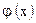й  и 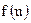 . Переменная  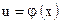называется промежуточным аргументомсложной функции.

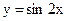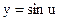Пример 6.  Þ  и  .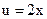

Сложная функция может иметь несколько промежуточных аргументов.