Скалярное произведение векторов.
Определение: Под скалярным произведением двух векторов  и
и 
понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е.  =
=
 ,
,  - угол между векторами
- угол между векторами  и
и  .
.
Скалярное произведение в координатной форме имеет вид:  , где
, где  и
и  .
.
Пример: Найти скалярное произведение векторов 
 и
и
Решение: 
Свойства скалярного произведения:
1.  ·
·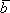 =
=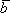 ·
· - коммутативность;
- коммутативность;
2.  ·(
·(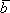 +
+ )=
)= ·
·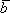 +
+ ·
· - дистрибутивность;
- дистрибутивность;
3. k·( ·
·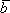 )=(k·
)=(k· )·
)·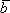 ,
,
4.  ·
· =
= 2
2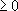 ,
,  2=0
2=0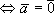 .
.
Определение 3. Углом между двумя ненулевыми n-мерными векторами называется угол, косинус которого вычисляется по формуле
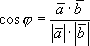 .
.
3) Условие коллинеарности и ортогональности векторов.
Определение 1. Два n-мерных вектора  и
и 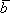 называются коллинеарными, если найдется число
называются коллинеарными, если найдется число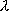 такое, что
такое, что =
=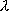 ·
·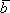 .
.
Рассмотрим два коллинеарных вектора  и
и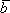 . Так как они коллинеарны, то
. Так как они коллинеарны, то =
=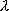 ·
·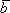 , или (a1, a2, …, an)=( b1, b2, …, bn ). Следовательно, a1= b1, a2= 2, …, an= bn.
, или (a1, a2, …, an)=( b1, b2, …, bn ). Следовательно, a1= b1, a2= 2, …, an= bn.
Выражая из этих равенств , получим
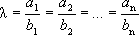 - условие коллинеарности.
- условие коллинеарности.
Для того чтобы два вектора были коллинеарными, необходимо и достаточно, чтобы их координаты были пропорциональны.
Найдем угол между коллинеарными векторами.
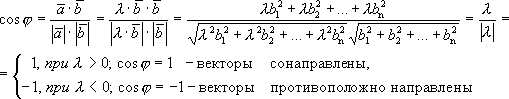 .
.
Определение 2. Два ненулевых n-мерных вектора  и
и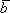 называются ортогональными, или перпендикулярными, если угол между ними равен 90°.
называются ортогональными, или перпендикулярными, если угол между ними равен 90°.
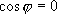 ,
,
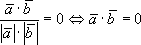 - условие ортогональности
- условие ортогональности

