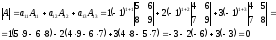Определители.
Определителем называется квадратная числовая таблица, вычисляемая по определенным правилам.
Пример Если 
, то
. Так
.
Если 
, то
.
Так 
.
Если 
, то
. Так
.
При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников. С плюсом берутся произведения элементов стоящих на главной диагонали и элементы, стоящие в вершинах следующих треугольников.
С минусом берутся произведения элементов, стоящих на второй диагонали и в вершинах следующих треугольников.
Второй метод заключается в том, что рядом с определителем справа записываются первый и второй столбцы и тогда с плюсом берутся произведения элементов, стоящих на главной диагонали и двух ей параллельных, с минусом – произведения элементов, стоящих на второй диагонали и двух ей параллельных.
Вычисление определителей более высоких порядков осуществляется путем использования их свойств.
Свойства определителей.
Пусть дана квадратная матрица 
Из элементов этой матрицы можно составить определитель, который называется детерминантом матрицы 
и обозначается
Минором 
некоторого элемента определителя 
называют определитель, который получается вычеркиванием из него
строки и
столбца. Например
, 
.
Алгебраическим дополнением элемента 
определителя называют число
. Например
, 
.
Свойства определителей.
1. Определитель не изменится, если его строки заменить столбцами и наоборот, т. е. 
.
2. Определитель меняет знак при перестановке любых двух его строк (столбцов).
3. Определитель, имеющий две равные строки (столбца), равен 0.
4. Общий множитель строки (столбца) можно выносить за знак определителя, например
.
5. Если элементы какой-нибудь строки (столбца) представимы в виде суммы двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, например
6. Определитель не изменится, если к какой-нибудь строке (столбцу) прибавить соответствующие элементы другой строки (столбца), умноженные на некоторое ненулевое число.
(I=I+II).
7. Определитель треугольной матрицы равен произведению её диагональных элементов.
8. Определитель равен сумме произведений элементов какой-нибудь его строки (столбца) на их алгебраические дополнения.
Например
.
Для вычисления определителя мы использовали разложение по второй строке, так как она содержит большее число нулевых элементов.
9. Сумма произведений элементов какой-нибудь строки (столбца) на соответствующее алгебраическое дополнение другой строки (столбца) равна 0.
Минором элемента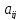 
называется определитель, составленный из элементов, оставшихся после вычеркиванияi-ой стоки и j-го столбца, на пересечении которых находится этот элемент. Минор элемента 
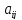определителяn-го порядка имеет порядок (n-1). Будем его обозначать через 
.
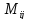Пример Пусть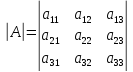 
, тогда
.
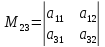Этот минор получается из A путём вычёркивания второй строки и третьего столбца.
Определение. Алгебраическим дополнением элемента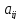 
называется соответствующий минор, умноженный на
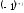т.е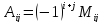
, гдеi –номер строки и j -столбца, на пересечении которых находится данный элемент.
VІІІ. (Разложение определителя по элементам некоторой строки). Определитель равен сумме произведений элементов некоторой строки на соответствующие им алгебраические дополнения.
.
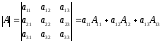Пример. Пусть 
, тогда
,
.
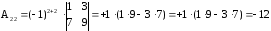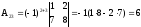Пример . Найдём определитель матрицы 
, разложив его по элементам первой строки.
