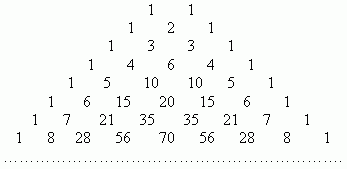Кратность - число появлений каждого элемента.

В общем случае число упорядоченных выборок = Arn среди них имеются размещения, содержащие одни и те же элементы, различающиеся только порядком их расположения.
Любую совокупность элементов можно переставить Pr c n-ми. Поэтому, если не учитывать порядок расположения, то число сочетаний будет в Pr раз меньше, чем число размещений.
Свойства числа сочетаний:
- Crn= 0, если r >n
- C0n= Cnn= 1
- Crn= Crn-1+Cr-1n-1
- Crn= Cn-rn

Бином Ньютона:
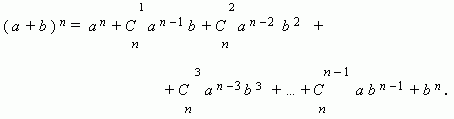


Числа 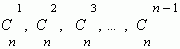 называются биномиальными коэффициентами.
называются биномиальными коэффициентами.
Геометрическая интерпретация 3го свойства Crn= Crn-1+Cr-1n-1
С помощью диаграмы треугольник Паскаля
Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля: