23 Теорема Гаусса в интегральной

Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду. 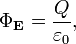Где 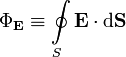— поток вектора напряжённости электрического поля через замкнутую поверхность S. Q — полный заряд, содержащийся в объёме, который ограничивает поверхность S. ε₀ — электрическая постоянная. Данное выражение представляет собой теорему Гаусса в интегральной форме. Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности.

24 Теорема Гаусса в диффер форме

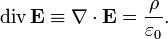 Здесь ρ — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а  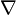— оператор набла.Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона (см. ниже). Формула однако также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте ее логичнее называть законом Гаусса^[

26 Уравнение Пуассона и лапласа

Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает электростатическое поле, стационарное поле температуры, поле давления, поле потенциала скорости в гидродинамике. Оно названо в честь знаменитого  французского физика и математика Симеона Дени Пуассона. Это уравнение имеет вид: Δφ = f,

где Δ — оператор Лапласа или лапласиан, а f — вещественная или комплексная функция на некотором многообразии. В трёхмерной декартовой системе координат уравнение принимает форму: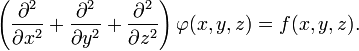В декартовой системе координат оператор Лапласа записывается в форме 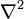и уравнение Пуассона принимает вид: 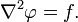Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона): Δφ = 0. Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».