Представьте, вы бросаете монету, вероятность успеха, например, выпадения герба есть p, вероятность неудачи q = 1 – p.
Посчитаем, сколько раз вам нужно бросить монету до появления первого успеха (первого герба).
Обозначим эту величину через  .
.
Очевидно, это случайная величина.
Зададимся вопросом: какое распределение имеет данная случайная величина?
Ответ прост: случайная величина n имеет геометрическое распределение, задаваемое формулой:
 ,
,
где k= 1, 2…
Гипергеометрическое распределение вероятностей
Пожалуй, второе по распространённости после биномиального распределения, в котором нет ничего гиперсложного. Да и сложного тоже. С гипергеометрическим законом распределения вероятностей мы неоднократно сталкивались ранее и фактически полностью построили в Примере 12 урока о классическом определении вероятности. Сформулируем задачу в общем виде и вспомним этот пример:
Пусть в совокупности из 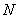 объектов содержатся
объектов содержатся 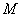 объектов, обладающие некоторым признаком. Из этой совокупности случайным образом и без возвращения извлекается
объектов, обладающие некоторым признаком. Из этой совокупности случайным образом и без возвращения извлекается 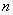 объектов. Тогда случайная величина
объектов. Тогда случайная величина 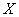 – количество «особых» объектов в выборке – распределена по гипергеометрическому закону.
– количество «особых» объектов в выборке – распределена по гипергеометрическому закону.
В ящике находится 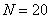 деталей, среди которых
деталей, среди которых 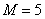 бракованных. Наудачу извлекаются
бракованных. Наудачу извлекаются 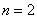 детали. Найти вероятность того, что:
детали. Найти вероятность того, что:
а) обе детали будут качественными;
б) одна деталь будет качественной, а одна – бракованной;
в) обе детали бракованны
По сути дела, здесь фигурирует случайная величина 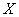 – количество бракованных деталей в выборке. Прорешаем данную задачу под другим углом зрения, а именно, найдём закон распределения этой случайной величины, которая, очевидно, может принять одно из следующих значений:
– количество бракованных деталей в выборке. Прорешаем данную задачу под другим углом зрения, а именно, найдём закон распределения этой случайной величины, которая, очевидно, может принять одно из следующих значений: 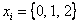 . Соответствующие вероятности
. Соответствующие вероятности 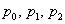 определяются правилами и формулами комбинаторики и классическим определением вероятности.
определяются правилами и формулами комбинаторики и классическим определением вероятности.
Сначала вычислим количество всех возможных наборов из 2 деталей. Две детали можно выбрать 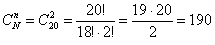 способами. Дальнейшие действия удобно занумеровать:
способами. Дальнейшие действия удобно занумеровать:
0) 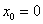 (в выборке нет бракованных деталей)
(в выборке нет бракованных деталей)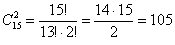 способами можно извлечь 2 качественные детали.
способами можно извлечь 2 качественные детали.
По классическому определению: 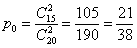 – вероятность того, среди 2 извлечённых деталей не будет бракованных.
– вероятность того, среди 2 извлечённых деталей не будет бракованных.
1) 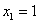
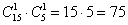 способами можно извлечь 1 качественную деталь и 1 бракованную.
способами можно извлечь 1 качественную деталь и 1 бракованную.
По тому же определению: 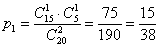 – вероятность того, среди 2 извлечённых деталей будет 1 бракованная.
– вероятность того, среди 2 извлечённых деталей будет 1 бракованная.
2) И, наконец, 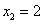
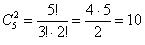 способами можно извлечь 2 бракованные детали.
способами можно извлечь 2 бракованные детали.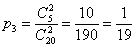 – вероятность того, что обе извлечённые детали будут бракованными.
– вероятность того, что обе извлечённые детали будут бракованными.
Таким образом, закон распределения количества бракованных деталей в выборке: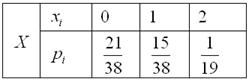
Контроль: 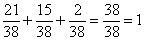
Следует отметить, что «зеркальная» случайная величина 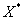 – количество качественных деталей в выборке, тоже имеет гипергеометрическое распределение. Догадайтесь с одного раза, как выглядит её закон распределения. НО, к этому вопросу нельзя подходить формально!
– количество качественных деталей в выборке, тоже имеет гипергеометрическое распределение. Догадайтесь с одного раза, как выглядит её закон распределения. НО, к этому вопросу нельзя подходить формально!
В частности, вероятность того, что герб выпадет на первом шаге равна 
Вероятность того, что герб выпадает впервые на втором шаге (а до того выпадала решетка), равна  и т.д.
и т.д.
Геометрическое распределение является частным случаем отрицательного биномиального распределения.
Геометрическая случайная величина обладает свойством отсутствия последействия: знание о том, что у вас не было успеха в течение n предыдущих бросков, никак не влияет на распределение оставшегося числа бросков до появления герба.
В непрерывном случае аналогом геометрической случайной величины является экспоненциальная случайная величина.
Распределение и формула Пуассона
http://mathprofi.ru/raspredelenie_i_formula_puassona.html
В данной статье мы рассмотрим ещё одно дискретное распределение, которое получило широкое распространение на практике. Не успел я открыть курс по теории вероятностей, как сразу стали поступать запросы: «Где Пуассон? Где задачи на формулу Пуассона?» и т.п. И поэтому я начну с частного применения распределения Пуассона – ввиду большой востребованности материала.
Задача до боли эйфории знакома:
– проводится 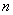 независимых испытаний, в каждом из которых случайное событие
независимых испытаний, в каждом из которых случайное событие 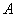 может появиться с вероятностью
может появиться с вероятностью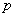 . Требуется найти вероятность того, что в данной серии испытаний событие
. Требуется найти вероятность того, что в данной серии испытаний событие 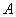 появится ровно
появится ровно 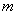 раз.
раз.
Наверное, вам уже снится формула Бернулли:)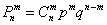
тем более, на уроке о биномиальном распределении вероятностей мы разобрали ситуацию по косточкам.
В том случае, если количество испытаний 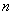 велико (сотни и тысячи), эту вероятность обычно рассчитывают приближённо – с помощью локальной теоремы Лапласа:
велико (сотни и тысячи), эту вероятность обычно рассчитывают приближённо – с помощью локальной теоремы Лапласа: 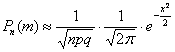 , где
, где 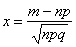 .
.
Однако и тут есть «слабое звено» – теорема Лапласа начинает серьёзно барахлить (давать большую погрешность), если вероятность 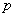 меньше, чем 0,1 (и чем меньше, тем всё хуже). Поэтому здесь используют другой метод, и именно распределение Пуассона.
меньше, чем 0,1 (и чем меньше, тем всё хуже). Поэтому здесь используют другой метод, и именно распределение Пуассона.
Итак, если количество испытаний 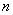 достаточно велико, а вероятность
достаточно велико, а вероятность 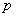 появления события
появления события 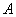 в отдельно взятом испытании весьма мала (0,05-0,1 и меньше), то вероятность того, что в данной серии испытаний событие
в отдельно взятом испытании весьма мала (0,05-0,1 и меньше), то вероятность того, что в данной серии испытаний событие 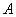 появится ровно
появится ровно 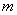 раз, можно приближенно вычислить по формуле Пуассона:
раз, можно приближенно вычислить по формуле Пуассона: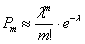 , где
, где 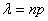
Напоминаю, что ноль факториал 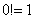 , а значит, формула имеет смысл и для
, а значит, формула имеет смысл и для 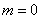 .
.
Вместо «лямбды» также используют букву «а».
Пример 1
В новом микрорайоне поставлено 10000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна 0,0002. Найти вероятность того, что за месяц откажет ровно 1 замок.
Утопичная, конечно, задача, но что делать – решаем:)
В данном случае количество «испытаний» 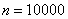 велико, а вероятность «успеха» в каждом из них – мала:
велико, а вероятность «успеха» в каждом из них – мала: 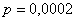 , поэтому используем формулу Пуассона:
, поэтому используем формулу Пуассона: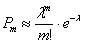
Вычислим: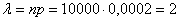 – по существу, это среднеожидаемое количество вышедших из строя замков.
– по существу, это среднеожидаемое количество вышедших из строя замков.
Таким образом: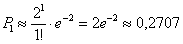 – вероятность того, что за месяц из строя выйдет ровно
– вероятность того, что за месяц из строя выйдет ровно 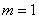 один замок (из 10 тысяч).
один замок (из 10 тысяч).
Ответ: