Существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью, — вытекает из уравнений Максвелла. Электромагнитные волны, обладая широким диапазоном частот (или длин волн лямбда=c/n, где с — скорость электромагнитных волн в вакууме), отличаются друг от друга по способам их генерации и регистрации, а также по своим свойствам. Поэтому электромагнитные волны делятся на несколько видов: радиоволны, световые волны, рентгеновское и гамма-излучения.
.png)
.png)
Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа:
.png)
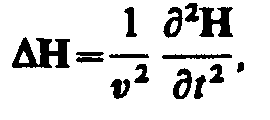
где 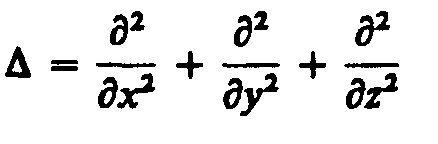 — оператор Лапласа, v — фазовая скорость.
— оператор Лапласа, v — фазовая скорость.
Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных воли определяется выражением:
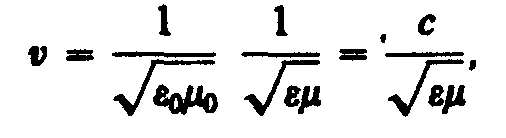
где с= 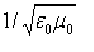 ,
, 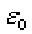 и
и  — соответственно электрическая и магнитная постоянные, e и m — соответственно электрическая и магнитная проницаемости среды.
— соответственно электрическая и магнитная постоянные, e и m — соответственно электрическая и магнитная проницаемости среды.
В вакууме (при .png) =1 и
=1 и  =l) скорость распространения электромагнитных волн совпадает со скоростью с. Так как
=l) скорость распространения электромагнитных волн совпадает со скоростью с. Так как .png)
 > 1, то скорость распространения электромагнитных воли в веществе всегда меньше, чем в вакууме.
> 1, то скорость распространения электромагнитных воли в веществе всегда меньше, чем в вакууме.
При вычислении скорости распространения электромагнитного поля по формуле получается результат, достаточно хорошо совпадающий с экспериментальными данными, если учитывать зависимость .png) и
и  от частоты. Совпадение же размерного коэффициента в со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электромагнитные волны.
от частоты. Совпадение же размерного коэффициента в со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электромагнитные волны.
Следствием теории Максвелла является поперечность электромагнитных волн: векторы Е и Н напряженностей электрического и магнитного полей волны взаимно перпендикулярны


