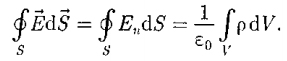- Циркуляция электростатического поля
Взаимодействие между покоящимися зарядами осуществляется через электрическое поле.Если все заряды, создающие поле, в данной системе отсчета неподвижны, то поле называется электростатическим.
Интеграл по замкнутому пути  называют циркуляцией вектора напряженности.
называют циркуляцией вектора напряженности.
Циркуляция вектора напряженности электрического поля вдоль любого контура равна нулю. Это утверждение называют теоремой о циркуляции вектора  .
.

Силовое поле, обладающее свойством 
, называют потенциальным.
Теорема о циркуляции вектора напряженности позволяет сделать вывод, что в электростатическом поле замкнутых линий вектора напряженности не существует: линии начинаются на положительных зарядах и кончаются на отрицательных (или уходят в бесконечность).
теорема Гаусса.
Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя выведенную немецким ученым К.Гауссом (1777 — 1855) теорему, определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность. В соответствии с формулой (79.3) поток вектора напряженности сквозь сферическую поверхность радиуса г, охватывающую точечный заряд Q, на- ходящийся в ее центре (рис. 126), равен
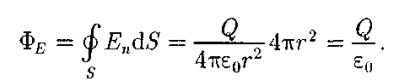

Если замкнутая поверхность произ- вольной формы охватывает заряд (рис. 127), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в нее, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее. Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен — ,т. е.

Знак потока совпадает со знаком заряда Q. Рассмотрим общий случай произвольной поверхности, окружающей п зарядов. В соответствии с принципом суперпозиции (80.2) напряженность Ё поля, создаваемого всеми зарядами, равна сумме напряженностей
 полей, создаваемых каждым зарядом в отдель- ности:
полей, создаваемых каждым зарядом в отдель- ности:


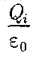 . Следовательно,
. Следовательно, 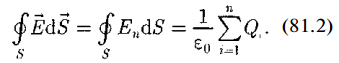
 различной в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, охватывающей некоторый объем V, равен
различной в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, охватывающей некоторый объем V, равен 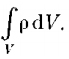 Используя этот результат, теорему Гаусса (81.2) можно записать так:
Используя этот результат, теорему Гаусса (81.2) можно записать так: