34. Вынужденные колебания. Дифференциальное уравнение и его решение на примере колебательного контура. Режимы установления колебаний и установившихся колебаний.

Вынужденными колебаниями наз. незатухающие колебания системы, которые вызываются действием внешней периодической силы. Если сила не будет периодической, то не возникнет и периодических колебаний. Например, если сила постоянна, то возникает статическое отклонение системы.

Примеры: колебания гребных винтов, лопаток турбины, качелей при раскачивании, мостов и балок при ходьбе и т.д.

Сила, вызывающая вынужденные колебания, наз. вынуждающей (возмущающей) силой.

Если внешняя вынуждающая сила изменяется по гармоническому закону , то в системе устанавливаются гармонические колебания с частотой внешней вынуждающей силы (процесс установления колебаний изображен на рисунке: вынужденные колебания накладываются на свободные затухающие колебания; после того, как свободные колебания прекращаются, остаются только вынужденные).

Запишем следующие формулы для вывода электромагнитных колебаний, учитывая, что  и :

;  ;

Тогда получим:

 ;

Продифференцировав по t , найдем силу тока при установившихся колебаниях.

 (*)

Где

Выражение (*) можно переписать в виде:

Где – сдвиг по фазе между током и приложенным напряжением. Тогда получим:

Из данной формулы видно, что ток отстает по фазе от напряжения , если , и опережает напряжение , если .

Пусть на некоторую материальную систему с непрерывно распределенными параметрами действует внешняя периодическая сила с частотой ω, то с течением времени в системе устанавливаются колебания с частотой внешней силы  ω. Имеется также следующее уравнение акустики :  (**) . Пусть . Если в системе установились колебания с частотой ω вынуждающей силы, то функцию  можно искать в виде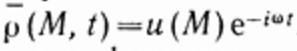

Подставляя данную функцию в (**) и сокращая на множитель , получим уравнение.

 (***)

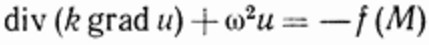В частности, в случае однородной среды коэффициент 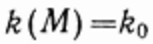 постоянный и уравнение (***) примет следующий вид:

 (****)

Где , . Уравнения (***) и (****) называются волновыми уравнениями, или уравнениями Гельмгольца.