33. Понятие декремента, логарифмического декремента, добротности колебательной системы на примере реального колебательного контура.

Декремент затухания  (от лат. decrementum - уменьшение, убыль) (логарифмический декремент затухания) – количественная характеристика быстроты затухания колебаний в линейной системе; представляет собой натуральный логарифм отношения двух последующих максимальных отклонений колеблющейся величины в одну и ту же сторону. T. к. в линейной системе колеблющаяся величина изменяется по закону  (где постоянная величина  - коэф. затухания) и два последующих наиб. отклонения в одну сторону X1 и X2 (условно наз. "амплитудами" колебаний) разделены промежутком времени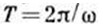 (условно наз. "периодом" колебаний), то  , а Д. з. будет равен – .

Так, напр., для механической. колебательной системы, состоящей из массы т, удерживаемой в положении равновесия пружиной с коэф. упругости k и испытывающей трение силой FT, пропорциональной скорости v (FТ =-bv, где b - коэф. пропорциональности), Д. з.

При малом затухании  . Аналогично для электрического контура, состоящего из индуктивности L, активного сопротивления R и ёмкости С, Д. з.

.

При малом затухании .

Для нелинейных систем закон затухания колебаний отличен от закона  , т. е. отношение двух последующих "амплитуд" (и логарифм этого отношения) не остаётся постоянным; поэтому Д. з. не имеет такого определенного смысла, как для систем линейных.

Добротность колебательной системы - безразмерный коэффициент, величина которого характеризует резонансные свойства линейной колебательной системы, отношение запасённой в системе энергии W к мощности потерь Р за период колебаний, т. е. Q = 2πωW / P. Теоретически определяется путём условного разграничения диссипативных (рассеивающих эл. энергию в тепло) и реактивных элементов. Практически часто измеряется как отношению резонансной частоты ω к ширине резонансной кривой Δω на уровне убывания амплитуды в ~ 2 раза: Q = ω/Δω, что характерно для Гауссова распределения спектра частот уединенного резонатора.

В случае электрических контуров запасённую энергию считают сосредоточенной в чисто реактивных элементах индуктивности L и ёмкости С, а потери связывают с протеканием тока по чисто диссипативному элементу - сопротивлению R. Тогда

В колебательных системах с большой добротностью частота и коэффициент затухания a слабозатухающих колебаний вида e-atsinωt связаны с добротностью отношением Q=ω/2a = p/d >> 1, где d = 2pa/ω  – декремент затухания. Добротность характеризует избирательную и разрешающую способности колебательной системы: чем больше Q, тем выше резонансный отклик системы по сравнению с нерезонансным; отклики системы на одинаковые по амплитуде сигналы с близкими частотами ω1 и ω2 существенно различны по величине и, следовательно, могут быть разрешены, если |ω1 - ω2|/Δω = ω/Q. Обычные радиоконтуры обладают добротностью Q~10-102, для камертона Q~102, для пьезокварцевой пластинки Q~2.104на частоте 20 кГц, для СВЧ-резонаторов Q~103-104, а для квазиоптических и оптических резонаторов Q~106-107. Если в системе существует несколько источников диссипации, то для получения результирующей добротности QS складываются обратные величины: