Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями.
Например, в случае механических гармонических колебаний:
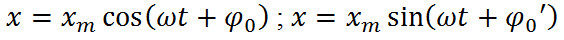
В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 + π/2 полностью совпадают.
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0.
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: 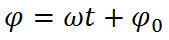 . Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.
. Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
Колебательный контур – цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью C и резистора сопротивлением R.
Согласно закону Ома: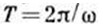
Где IR – напряжение на резисторе,  – напряжение на конденсаторе,
– напряжение на конденсаторе,
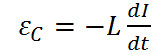 – э.д.с. самоиндукции, возникающая в катушке при протекании в ней переменного тока (
– э.д.с. самоиндукции, возникающая в катушке при протекании в ней переменного тока ( 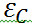 – единственная э.д.с. в контуре). Следовательно,
– единственная э.д.с. в контуре). Следовательно,
.jpg)
Разделив данное выражение на L и подставив 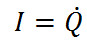 и
и  , получим дифференциальное уравнение колебаний заряда Q в контуре:
, получим дифференциальное уравнение колебаний заряда Q в контуре:

В данном колебательном контуре внешние э.д.с. отсутствуют, поэтому рассматриваемые колебания представляют собой свободные колебания. Если сопротивление R=0, то свободные электромагнитные колебания в контуре являются гармоническими. Тогда получим дифференциальное уравнение свободных гармонических колебаний заряда в контуре:
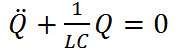
Тогда получается, что заряд Q совершает гармонические колебания по закону
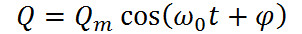
Где – 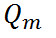 амплитуда колебаний заряда конденсатора с циклической частотой
амплитуда колебаний заряда конденсатора с циклической частотой 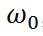 , называемой собственной частотой контура, т.е.
, называемой собственной частотой контура, т.е.

И периодом
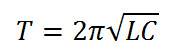
Данная формула впервые была получена У.Томпсоном и называется формулой Томпсона.
Сила тока в колебательном контуре
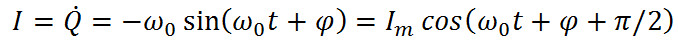
Где  – амплитуда силы тока.
– амплитуда силы тока.
Напряжение на конденсаторе
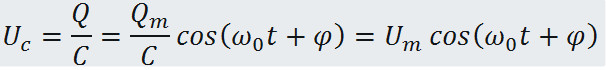
Где .jpg) – амплитуда напряжений.
– амплитуда напряжений.
Тогда получается, что колебания тока I опережают по фазе колебания заряда Q на 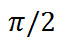 , т.е., когда ток достигает максимального значения, заряд (а также и напряжение) обращается в нуль, и наоборот.
, т.е., когда ток достигает максимального значения, заряд (а также и напряжение) обращается в нуль, и наоборот.

